Poiseuille flow with variable viscosity test cases (2D/3D)
Poiseuille flow with variable viscosity test cases (2D/3D)
This test case solves the 2D/3D Poiseuille flow in a rectangular channel at \( Re=100 \) with a viscosity variable viscosity in space. The aim of this test case is to validate the discretization of the Stokes / Navier-Stokes equations with variable viscosity.
Domain is square, its opposite corner coordinates being \((0,0,0)\) and \((0.02,0.02,0.02)\). We solve the Navier-Stokes equations on the whole domain. The exact velocity profile is imposed on left boundary condition, Neumann boundary condition is set on the right, wall are set on top and bottom boundaries, symmetry or periodic on front and back one;
If \( h \) is the halft height of the domain, viscosity is given by:
\( \mu \ = \ \mu_0 \ e^{a^2 \frac{(y -h)^2}{h^2}} \) with \( \mu_0 = 1.85 \ 10^{-5} \) and \( a=2 \).
Solution is given by:
\( u \ = \ \frac{k e^2 e^{-a^²}}{2 a^2 \mu_0} \ (e^{a^2 (1 - \frac{(y -h)^2}{h^2})} \ - \ 1) \) with \( k=0.25 \).
Navier-Stokes equation are used:
Second order spatial convergence is expected.
To check the symmetry of the code, inlet can be imposed on bottom or back boundaries. Same solution should be observed up to computer precision. This is done and checked in the validation script of Notus. Spatial convergence is done on the Poiseuille flow in the \( x \) direction.
The grid size starts from 10 in every direction to 80. Viscosity and \( u \) velocity component vertical profiles for a \( 128x128 \) grid are shown Figures 1. The 2D velocity vectors are shown Figure 2. Second order convergence is observed with \(L_2\), \(L_1\) or \(L_\infty\) norms and regular meshes (see Tables below).
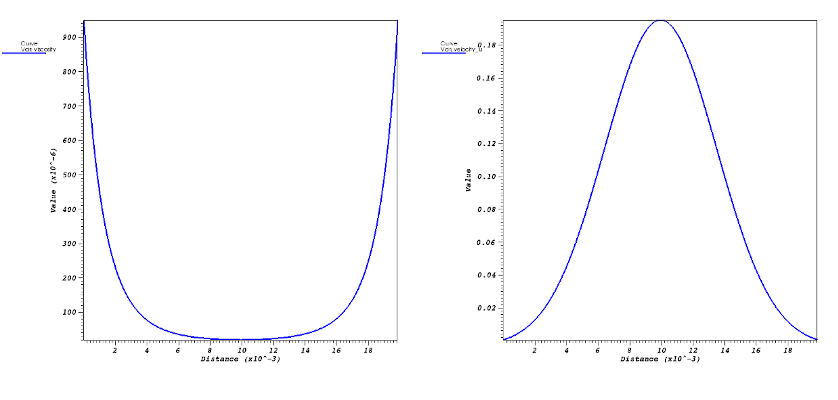
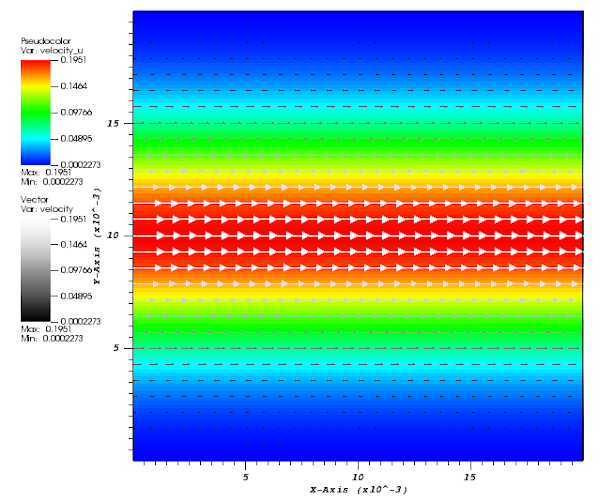
2D results
| Mesh | Order | Order | Order | |||
|---|---|---|---|---|---|---|
| 20 | 3.894138e-04 | n/a | 7.420831e-08 | n/a | 3.529784e-06 | n/a |
| 40 | 1.045377e-04 | +1.897281 | 1.753025e-08 | +2.081735 | 8.935680e-07 | +1.981931 |
| 80 | 2.660690e-05 | +1.974151 | 4.238561e-09 | +2.048200 | 2.234279e-07 | +1.999768 |
| 160 | 6.541192e-06 | +2.024175 | 1.023849e-09 | +2.049572 | 5.468840e-08 | +2.030503 |
3D results
| Mesh | Order | Order | Order | |||
|---|---|---|---|---|---|---|
| 20 | 3.841166e-04 | n/a | 1.462917e-09 | n/a | 4.921641e-07 | n/a |
| 40 | 1.031185e-04 | +1.897241 | 3.457121e-10 | +2.081205 | 1.246385e-07 | +1.981389 |
| 80 | 2.623945e-05 | +1.974494 | 8.358327e-11 | +2.048285 | 3.117087e-08 | +1.999480 |