Validation of the 2D turbulent flat plate flow with RANS standard and SST version of k-omega model.

This test case simulates the 2D incompressible turbulent flow over a flat plate with RANS model (Reynolds-Average Navier-Stokes) \( k-\omega \). The configuration is based on the well-documented benchmark from NASA [1], which presents a 2D zero-pressure-gradient flat plate of length \( L = 2 \) m. Dimensionless number values are for Reynolds number based on half plate length \(\mathrm{Re}= u_{\infty} (L/2) / \nu = 5\cdot 10^{6}\), for Mach number \(\mathrm{Ma}=u_{\infty} / c_s =0.2\), for Prandtl number \(\mathrm{Pr} = c_p \mu / \lambda = 0.71 \). A unity fluid (air) is used with density \( \rho_{\infty} = \) 1 \( kg/m^3 \), kinematic viscosity \( \nu = u_{\infty}(L/2) /\mathrm{Re} = 1.39 \cdot 10^{-5} \), specific heat capacity at constant pressure \(c_p= 1004.5 \) J/kg/K and conductivity \( \lambda = \mu c_p / \mathrm{Pr} = 1.96 \cdot 10^{-2}\) W/m/K.

The freestream conditions for velocity, turbulent kinetic energy and specific dissipation rate are the following \( u_{\infty} = 69.26 \) m/s, \( k_{\infty} = 1.08 \cdot 10^{-3} m^2/s^2\) and \( \omega_{\infty} = 8.68 \cdot 10^{3} \) 1/s.

We compare Notus implementation of standard k- \(\omega \) (labeled STD) [3] and SST k- \(\omega \) (labeled SST) [4] against two independent compressible RANS codes (CFL3D and FUN3D) with k- \(\omega \) klim-m version (data extracted from NASA website [1]). The present validation ensures the accuracy and the reliability of the turbulence k- \(\omega \) models implemented in Notus.

Configurations

The boundary conditions are chosen as follows:

\( (u,v) \) :

\( k \) :

\( \omega \) :

The initial conditions are chosen as follows:

\( k_0 = k_{\mathrm{\infty}} \) : \( \omega = \omega_{\mathrm{\infty}} \), \( (u_0,v_0) = (u_{\mathrm{\infty}},0) \).

Mesh grid

Results are presented on the converged grid 707x384 with a composite mesh refinement. Along the vertical axis, two exponential meshes with different factors are applied. The first cell has \( \Delta y = 5 \cdot 10^{-7} \) m at the wall. Along the horizontal axis, the domain is divided into four zones:

• The first zone, located before the leading edge, features a coarser exponential mesh.
• The second zone, near the leading edge, is finely discretised with a uniform mesh.
• The third zone is a transitional area with an exponential mesh extending to the midpoint of the plate.
• Lastly, the fourth zone applies a coarser uniform mesh over the remaining half of the plate.

Figure 1: Composite mesh 707x384, \( \Delta y = 5 \cdot 10^{-7}\) m.

Runtime parameters

Main parameters to run this test case are:

• Incremental pressure correction method for incompressible flows
• BDF2 second order temporal scheme
• HYPRE with boomeramg preconditioner for momentum, smg preconditioner for pressure, k and omega

Simulations stop when velocity stationnary reached a absolute tolerance of \(1 \cdot 10^{-6}\).

Comments

The validations of SST version of k- \(\omega \) [4] is performed in the following. For comparison purpuse, we also present results from the standard version [3] of k- \(\omega \) model to asses its accuracy on this test-case.

Special attention has been paid to the selection of boundary conditions for the RANS variables k and omega, especially for the \( \omega_{\mathrm{wall}} \) boundary condition. The values found in various references exhibit significant discrepancies, sometimes of several order of magnitudes. Several boundary conditions were tested, but chosen boundary conditions are the following (provided but [1] and but the OpenFOAM user notes [5] available on the NASA website [1].

\( k_{\mathrm{\infty}}= 9 \cdot 10^{-9} c_s^2\) \( m^2/s^2\),

\( \omega_{\mathrm{\infty}}= 1 \cdot 10^{-6}\frac{\rho c_s^2}{\mu} \) \( s^{-1}\),

\( \omega_{\mathrm{wall}}= 10 \frac{6 \nu}{\beta_1 \Delta y^2} \) \(s^{-1}\),

with the sound speed \(c_s = 347.19\) m/s and \( \beta_1=0.075\) a model constant.

Results

For \( x = 0.9708 \), Figure 2 and 3 shows respectively velocity normalized by friction velocity \( u^+ \) against the logarithm of \( y^+ \) and velocity normalized by the freestream velocity against \( y \). The results align well with classical wall law behavior. The viscous sublayer follows the expected relationship \( u^+ = y^+ \), and no deviations are seen in the logarithmic layer for the notus k- \(\omega \) SST implementation compared to CFL3D klim-m data [3].

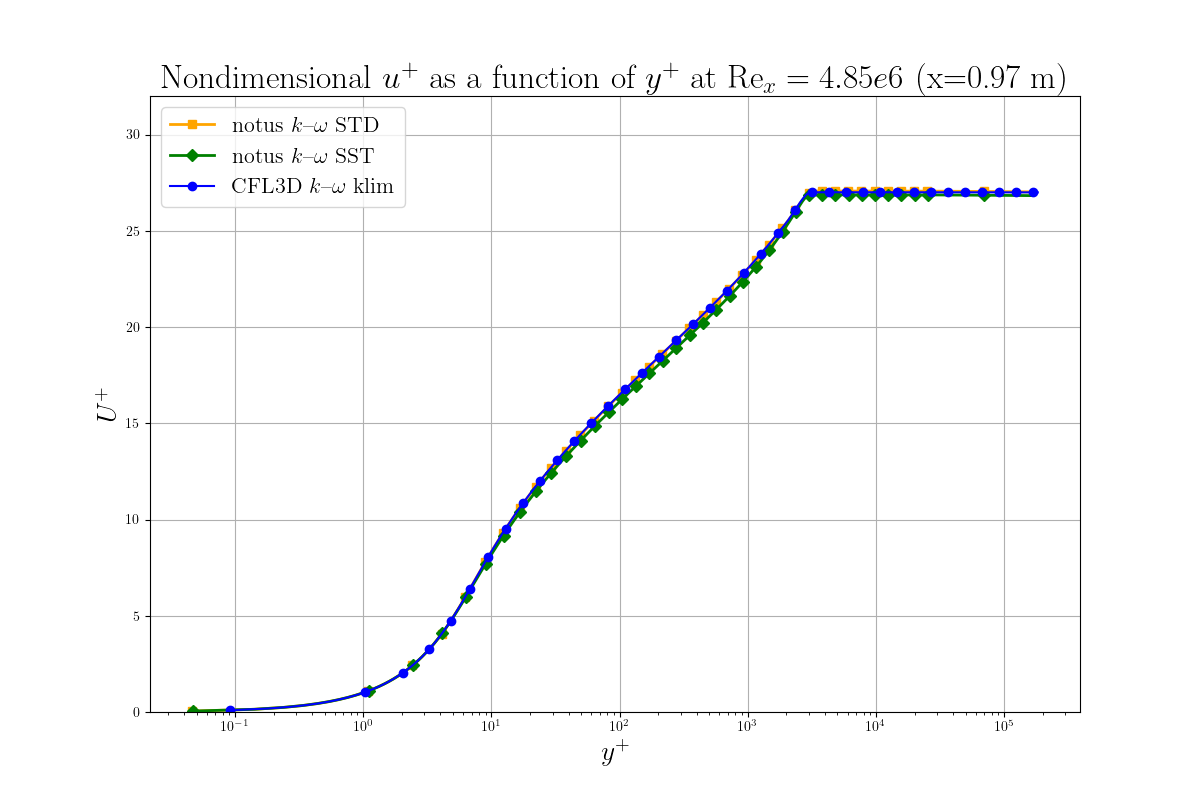
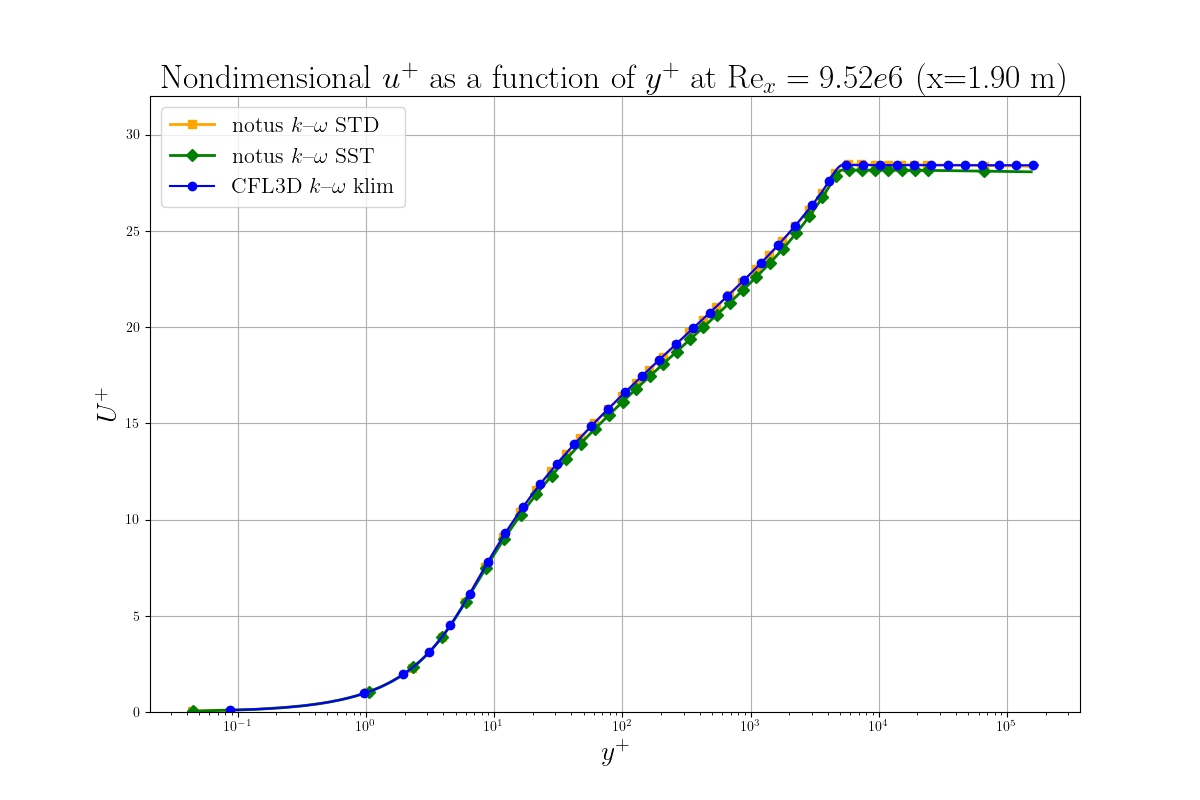
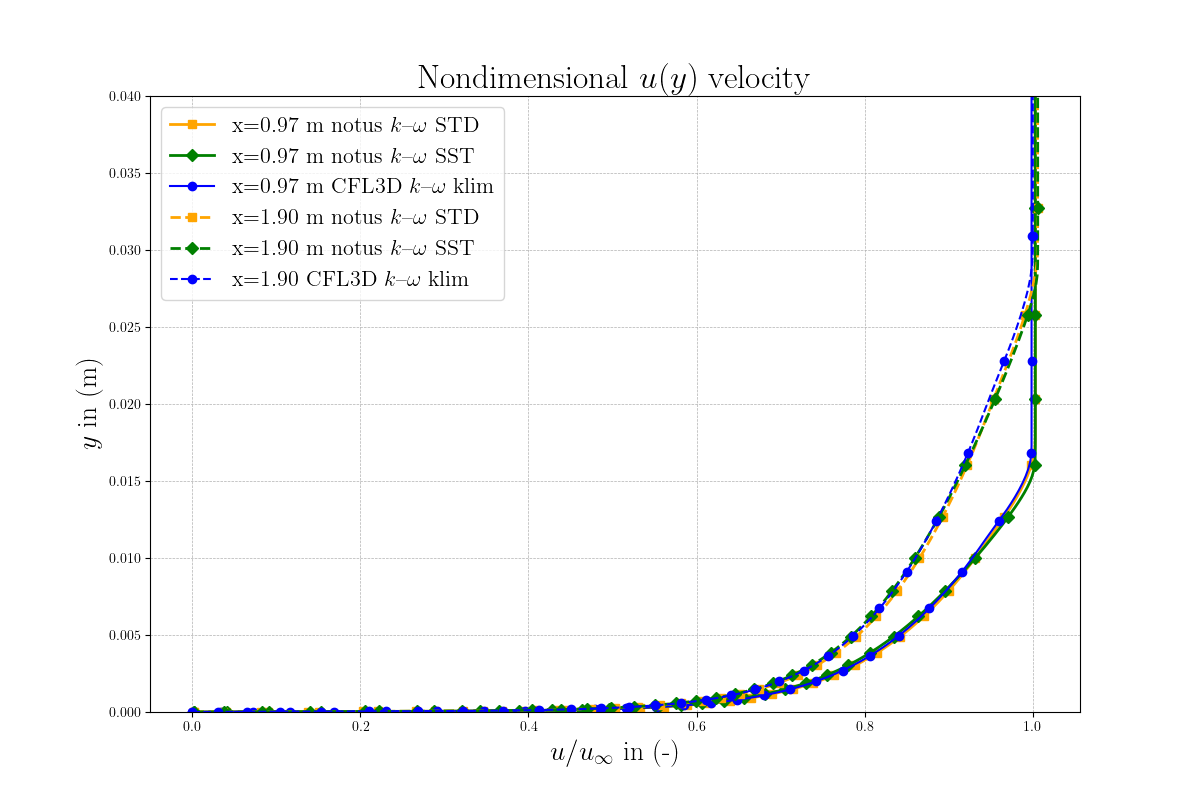
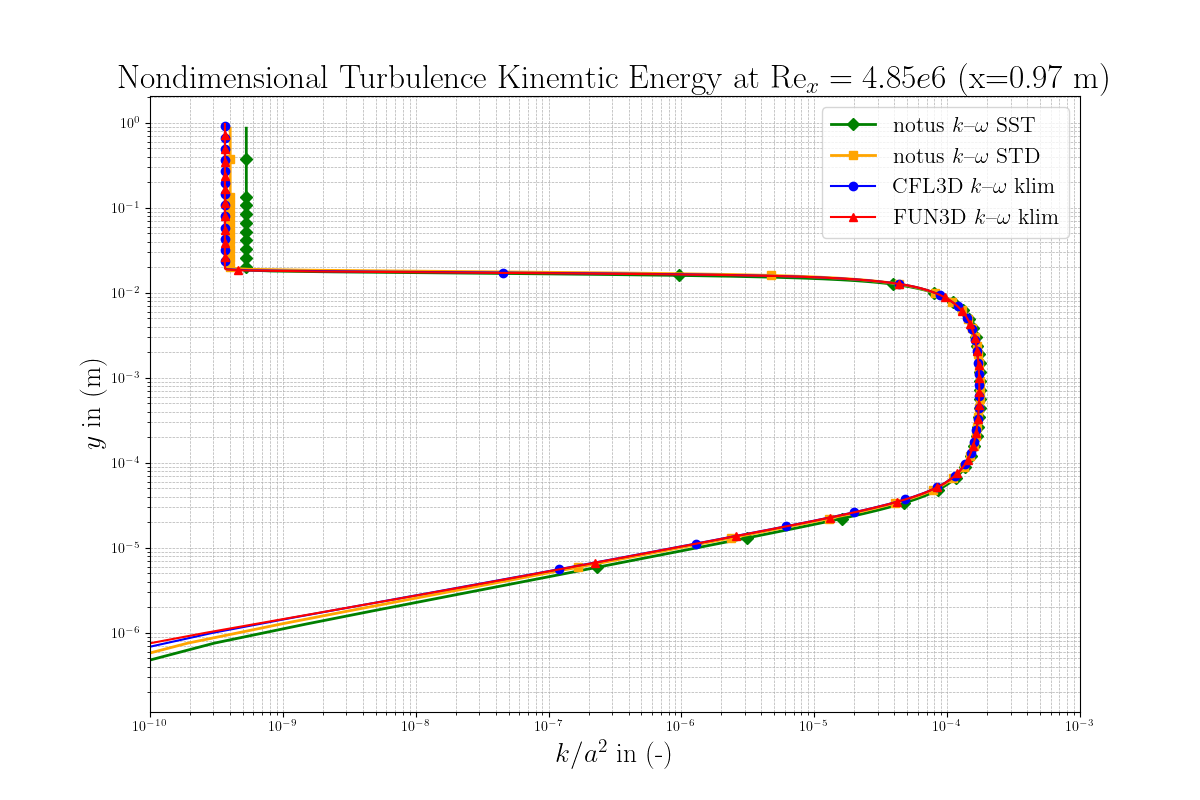
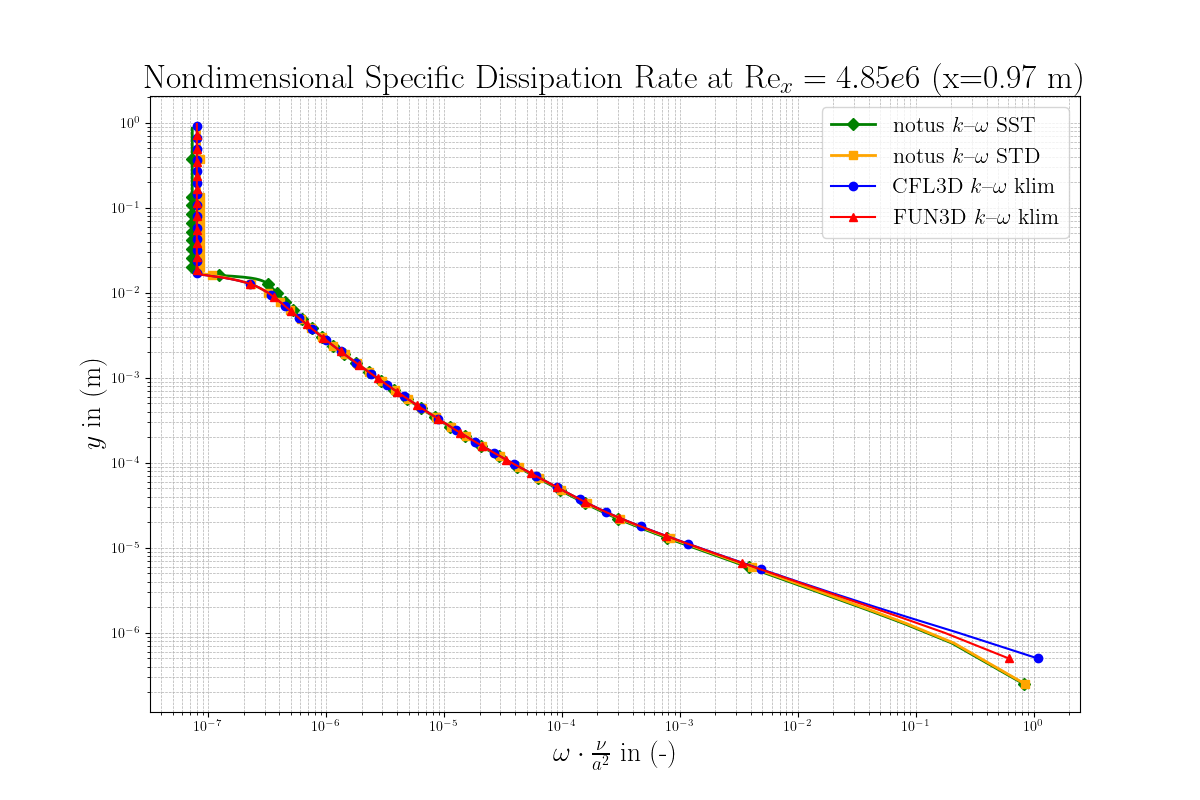
Then, for \(x = 0.97\) m, we plot respectively in Figure 4, 5, 6, the profiles of k, \(\omega\) and the dimensionless eddy viscosity. By comparing these results with those of NASA FUN3D and CFL3D klim-m implementation [1], we observe a very good agreement for the notus \(k \omega\) SST model. Note the discrepancies between STD and SST version of \(k \omega\).

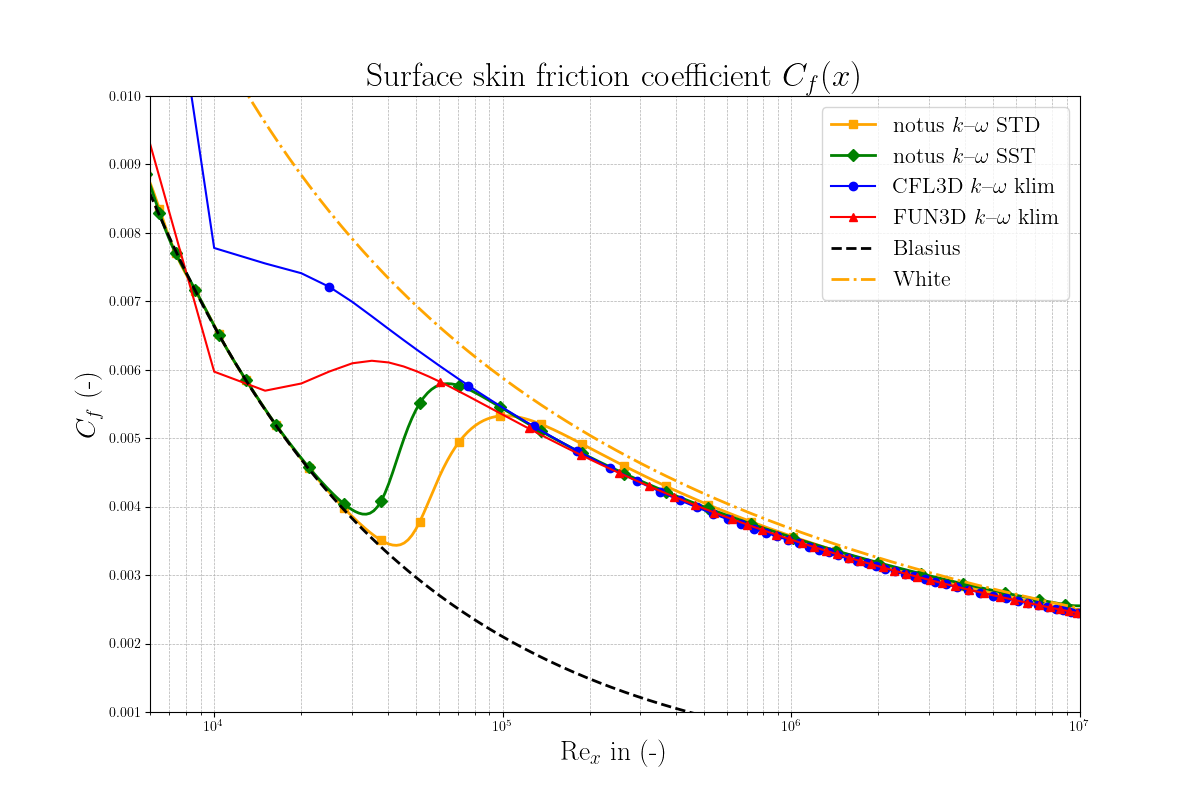
Finally, the local wall skin friction coefficient \( C_f(x) = \frac{2\tau_{\mathrm{wall}}}{\rho_{\infty} u_{\infty}^2} \) along the plate is shown in Figure 7, with \( \tau_{\mathrm{wall}}(x) \) the wall shear stress at position \( x\). Blasius and White local wall skin friction coefficient formulas [2] are added to the Figure. We note the good agreement of notus implementation of k- \(\omega \) SST with CFL3D and FUN3D klim-m [1] and White forumla in the turbulent region between \( \mathrm{Re}_x \in [10^{6}, 10^{7}] \).

References

[1] NASA, 2D Zero Pressure Gradient Flat Plate Verification Case, Wilcox2006-klim-m Expected Results, https://turbmodels.larc.nasa.gov/flatplate_w06.html

[2] F. White (2011). Fluid Mechanics. New York City, NY: McGraw-Hill. pp. 477–478.

[3] D. C., Wilcox. Formulation of the k-w Turbulence Model Revisited. AIAA Journal, (46):2823–2838, 2008

[4] F. R. Menter. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal, 32(8):1598–1605, 1994

[5] S. Gomez, S.V. Poroseva, Changes and Settings for Standard Turbulence Model Implementation in OpenFOAM, , Mechanical Engineering, University of New Mexico, https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4748366.