MOF test case for 5 materials with sheared velocity field

This test case simulates a domain with five fluids. The aim is using the B-tree technique in MOF method.

The verification criteria is:

• The main volume fraction;
• The symmetric difference area.

Configurations

Physical domain and geometry

The simulations take place in a box of fluid of coordinates (0,0) and (1,1). The four fluids are placed in four circles of radius 0,15 divided into four portions. Each fluid occupies one portion of each circle.

Fluids' properties

All the fluids considered have the same properties :

where \(\rho\) is the density, \(\mu\) the dynamic viscosity coefficient, \(\sigma\) the conductivity, C the specific heat capacity, \(\alpha\) the thermal expansion coefficient and \(T_{0}\) the reference temperature.

Velocity field

The velocity field is in the sheared case . The velocity is given as: \(u(x,y)=(\alpha (\sin(\pi x))^2 \sin(\pi y) \cos(\pi y) \cos( \dfrac{\pi t}{\tau} ),\alpha (\sin(\pi y))^2 \sin(\pi x) \cos(\pi x) \cos( \dfrac{\pi t}{\tau} ) )\) where \(\alpha \) and \(\tau \) are respectively the amplitude and the period.

Phase advection

The numerical method used for Phase advection is MOF.

Runtime parameters

Spatial discretization

The variable CellsPerDirection is used to change the regular mesh. We consider \(\dfrac{L}{\Delta x}=CellsPerDirection\) for each direction of the grid.

Time discretization

Time step is fixed and equals to \(10^{-3}s\). The final time is set to one period.

UseFilaments choice

The variable UseFilaments is used to toggle filaments in MOF method.

UseAnalyticReconstruction choice

The UseAnalyticReconstruction variable is used to choose between the analytic reconstruction and minimization. The tolerance angle and derivative are respectively set to \(10^{-5}\) and 0.

B-tree method

Since the domain contains five materials, the B-tree method is used within MOF.

Comments

Using filaments is necessary in this test case, otherwise inconvenient results are found. Using filter is also recommended but disturbs the convergence.

Results

Numerical results

Figure 1 shows the volume fraction of the main fluids at three different times in the case of CellsPerDirection=128 with using filaments and analytic reconstruction. Figure 2 shows the volume fractions in the case of disabling filaments.

Figure 1: Volume fraction of the fluids at different times with CellsPerDirection=128

Figure 1: Volume fraction of the fluids at different times without using filamennts

Spatial convergence

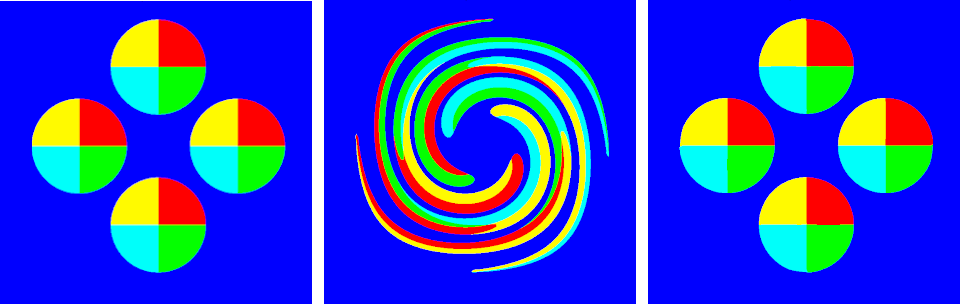
Four spatial discretizations are used to study the convergence of the mesh.