Laplacian test cases with Dirichlet boundary conditions (2D/3D)

This test case solves the 2D/3D Laplace equation with Dirichlet boundary conditions on 2 opposite boundaries. The aims of this test case are:

1. validate the discretization of the diffusive term of a cell advection/diffusion equation;
2. validate the Dirichlet boundary condition of a cell scalar equation;
3. validate the Neumann and periodic boundary conditions.

Configurations

Domain is rectangular, its opposite corner coordinates being \((0,0,0)\) and \((1,2,3)\). We solve \(- \Delta T=f\) on the whole domain. 1D solution of the problem is set to \(x^2\) (see figure below). The right-end-side term \( f \) is equal to \(-2\).

Figure 1: Elevation of the temperature field

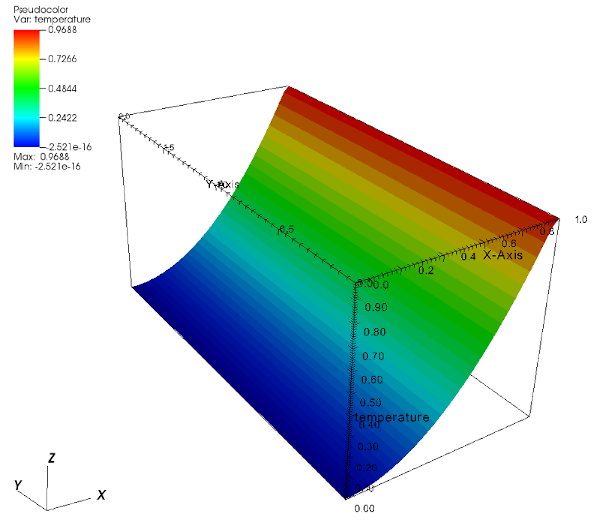
The global boundary conditions are chosen as follows.

Runtime parameters

Energy equation is used:

• temporal and inertial terms are disabled;
• MUMPS or HYPRE solvers can be used;
• linear or quadratic schemes for the boundary conditions are used.

The case is also testing the correctness of the resolution in the 3 directions.

Comments

Since the problem is 1D, whatever the direction considered solutions should be equal up to computer precision. This is verified is the validation script of Notus on one mesh.

As regards spatial convergence, since a centered second order scheme is used to discretize the Laplacian, we expect no error on the solution compared to the quadratic exact solution. This point is achieved only if a quadratic scheme is used to apply the boundary conditions (compared to a linear one).

Results

With quadratic scheme for the boundary conditions, the solution is reached up to computer precision whatever the mesh size.

A convergence sutdy is done if a linear scheme is used for the boundary conditions. The grid size starts from 10 in every direction to 160. Second order convergence is observed with \(L_2\), \(L_1\) or \(L_\infty\) norms.

2D results

3D results