3D channel flow simulation (periodic)

This test case solves the 3D flow in a rectangular section channel. The aims of this test case are to:

1. validate the discretization of the Stokes / Navier-Stokes equations with regular (or not) grids.
2. validate the boundary conditions implementations (Dirichlet, Neumann, Periodic)

Configurations

We solve the Navier-Stokes equations on the whole domain which opposite corner coordinates are \((0,0,0)\) and \((0.5,0.01,0.1)\). The air flow is forced thanks to a right-hand side pressure gradient on the u component of the equations equal to 0.186231521215612 that correspond to a Reynolds number \( Re = 53 \). In this case, periodicity is set on the x direction. Exact solution of the problem, depending on \(y\) and \(z\), is given in [1]:

\[ u(y,z) = 6 u_0 z(1 - z) + \frac{48}{\pi^3} \sum\limits_{n=0}^\infty \frac{(-1)^{n+1}\cosh[(2n+1)\pi(y-B/2)]\cos[(2n+1)\pi(z-1/2)]}{(2n+1)^3\cosh[(2n+1)\pi B/2]} \]

where H is the height of the domain, B the transversal aspect ratio \(l/H\) with \(l\) the channel width, and \(u_0\) the dimensional average velocity of the 2D Poiseuille flow ( \( u_0 = - \frac {H^2} {12 \mu} \frac{\partial p}{\partial x}\)).

Runtime parameters

Navier-Stokes equations are used if:

• the advection term is enable (second order centered scheme);
• HYPRE solvers are used.

Comments

Second order spatial convergence is expected on component \(u\) of the velocity field. Moreover, \(v\) and \(w\) components should be equal to \(0\).

To check the symmetry of the code, periodicity can be imposed on \(y\) or \(z\) direction. Same solution should be observed up to computer precision. This done and checked in the validation script of Notus. Spatial convergence is done on the Channel flow in the \( x \) direction.

Results

The grid size starts from 16 in every direction to 128. Figure below show the \(u\) velocity component for a \(16x16x16\) mesh.

Figure 1: u velocity component of the channel 3D flow

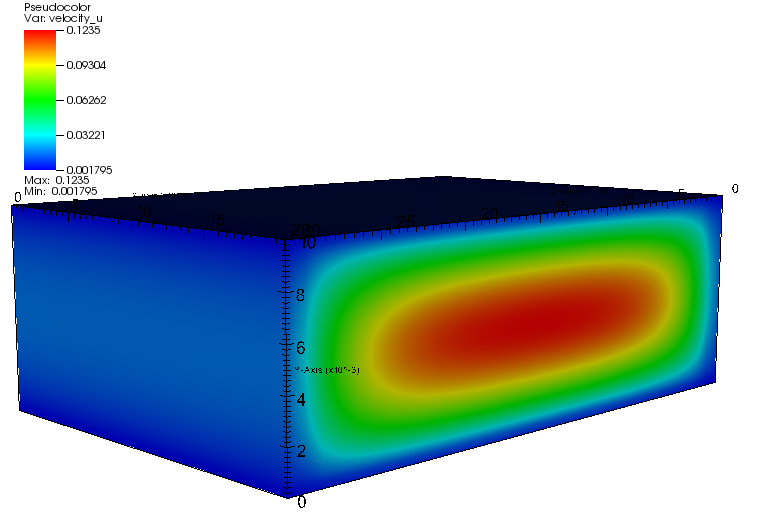
Second order convergence is observed with \(L_2\), \(L_1\) or \(L_\infty\) norms (see Table below). Moereover, \(v\) and \(w\) velocity components are equal to \(0\) up to the computer precision.

References

A. Benzaoui, X. Nicolas and S. Xin, Efficient vectorized finite difference method to solve the incompressible Navier-Stokes equations for the 3D mixed convection flows in high aspect ratio channels, Num. Heat Trans. B, 48, 277-302, 2005