This test case suite focuses on the immersed boundary applied to the Laplace equation.

This test case suite focuses on the immersed boundary applied to the Laplace equation with either Dirichlet or Neumann boundary conditions. The objectives of this test case are:

1. verify the core of the immersed boundary method.
2. verify the order of spatial convergence of the method.

Configurations

Physical domain

The global boundaries are defined by the box:

\begin{align} [-1, +1]^2 &\quad\text{in 2D,} & [-1, +1]^3 &\quad\text{in 3D.} \end{align}

The immersed boundary is either a cylinder or a sphere:

\begin{align} x^2 + y^2 = r_c^2 &\quad\text{(cylinder),} & x^2 + y^2 + z^2 = r_c^2 &\quad\text{(sphere),} \end{align}

where \(r_c = \frac{13}{20}\). The inner domain can be inside or outside the shape. Most cases set the inner domain outside.

Solutions

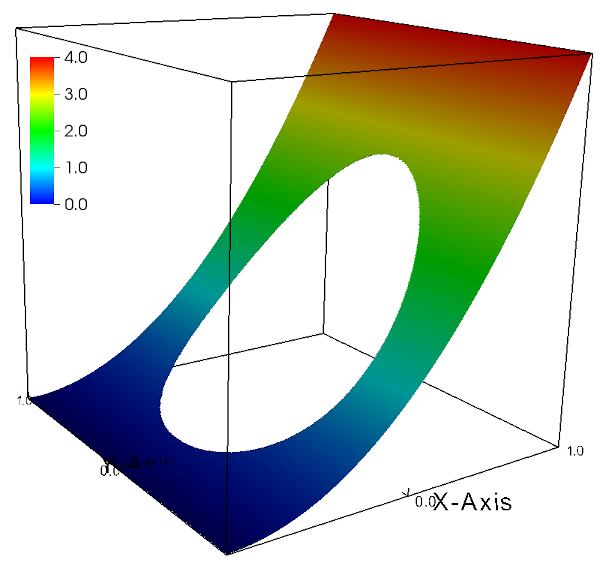
The source term and the boundary conditions are chosen to obtain the following solution:

\begin{align} T(x,y,z) = (1 + x)^2 \end{align}

in the inner domain. The source term is then

\begin{align} S(x,y,z) = 2. \end{align}

The average temperature can be computed analytically. First the volume of the inner domain must be known:

\begin{align} \begin{aligned} V &= 4 - \pi r_c^2 &&= 2.6726771038583124\ldots\quad\text{2D, outside} \\ V &= \pi r_c^2 &&= 1.3273228961416876\ldots\quad\text{2D, inside} \\ V &= 8 - \tfrac{4}{3}\pi r_c^3 &&= 6.8496534900105374\ldots\quad\text{3D, outside} \end{aligned} \end{align}

The average temperatures are thus obtained by:

\begin{align} V \bar{T} &= 2\int_{-1}^{-r_c}{T(x)^2{\rm d}x} + 2\int_{-r_c}^{+r_c}{1 - \sqrt{r_c^2-x^2}T(x)^2{\rm d}x} + 2\int_{+r_c}^{+1}{T(x)^2{\rm d}x} \quad\text{2D, outside} \\ V \bar{T} &= 2\int_{-r_c}^{+r_c}{\sqrt{r_c^2+x^2}T(x)^2{\rm d}x} \quad\text{2D, inside} \\ V \bar{T} &= 4\int_{-1}^{-r_c}{T(x)^2{\rm d}x} + \int_{-r_c}^{+r_c}{4 - \pi (r_c^2-x^2)T(x)^2{\rm d}x} + 4\int_{+r_c}^{+1}{T(x)^2{\rm d}x} \quad\text{3D, outside} \end{align}

The values are given in the table below.

Geometry	\(\bar{T}\)
2D, outside	\( 1.446419378796616\ldots \)
2D, inside	\( 1.105625 \) (exact value)
3D, outside	\( 1.375122973785438\ldots \)

Boundary conditions

The global boundary conditions are chosen as follows.

Boundary	Condition	Value
left	Dirichlet	\( T = 0 \)
right	Dirichlet	\( T = 4 \)
bottom	Neumann	\( \partial_{\mathrm n}T = 0 \)
top	Neumann	\( \partial_{\mathrm n}T = 0 \)
back	Neumann	\( \partial_{\mathrm n}T = 0 \)
front	Neumann	\( \partial_{\mathrm n}T = 0 \)

The immersed boundary conditions type are either Dirichlet or Neumann

Label	Condition type	Value
dirichlet	Dirichlet	\( T = (1+x)^2 \)
neumann	Neumann	\( \partial_{\mathrm n}T = 2 (1 + x) * n_x \)

Grids

There are the grid sizes used to perform validation tests.

Label	D's	Size
	2D	16×16
a2.8	2D	28×10
a7.6	2D	38×5
	3D	16×16×16
a	3D	32×14×9

Test case list

Label
laplacian_dirichlet
laplacian_dirichlet_a2.8
laplacian_dirichlet_a7.6
laplacian_neumann
laplacian_neumann_o2
laplacian_dirichlet_inverted
laplacian_dirichlet_3D
laplacian_dirichlet_3D_a
laplacian_neumann_3D
laplacian_neumann_3D_o2

Runtime parameters

The following common setting are used:

• The temporal term of the energy equation is deactivated.
• The MUMPS solver is used by default.
• No stop test are performed and just one iteration is done.

Results

Here are the actual results of convergence order. The temperature field is compared to the reference solution to yield errors in the three norms. The order of convergence is computed for each criterion.

laplacian_dirichlet

Mesh	\(L^\infty\) error	Order	\(L^1\) error	Order	\(L^2\) error	Order	\(\bar{T}\)	Order
16	3.79715746e-03	n/a	6.92031431e-03	n/a	4.49087047e-03	n/a	1.44196504	n/a
32	9.62446241e-04	+1.9801	2.06159123e-03	+1.7471	1.28891146e-03	+1.8008	1.44513690	n/a
64	2.50782544e-04	+1.9403	4.58485032e-04	+2.1688	2.91641181e-04	+2.1439	1.44612847	+1.6776
128	6.30554132e-05	+1.9917	1.20982603e-04	+1.9221	7.63063860e-05	+1.9343	1.44634302	+2.2084
256	1.64327857e-05	+1.9400	2.99587136e-05	+2.0138	1.89250382e-05	+2.0115	1.44640090	+1.8904
512	4.29627841e-06	+1.9354	7.45031545e-06	+2.0076	4.69627061e-06	+2.0107	1.44641472	+2.0657
1024	1.09421763e-06	+1.9732	1.90182459e-06	+1.9699	1.19557412e-06	+1.9738	1.44641820	+1.9885

laplacian_dirichlet_a2.8

Mesh	\(L^\infty\) error	Order	\(L^1\) error	Order	\(L^2\) error	Order	\(\bar{T}\)	Order
28	1.26609670e-03	n/a	2.85323449e-03	n/a	1.78043721e-03	n/a	1.44519082	n/a
56	3.18765249e-04	+1.9898	7.07233505e-04	+2.0123	4.39962582e-04	+2.0168	1.44610496	n/a
112	7.93554719e-05	+2.0061	1.67267705e-04	+2.0800	1.04266823e-04	+2.0771	1.44633962	+1.9619
224	2.33990991e-05	+1.7619	4.39922886e-05	+1.9268	2.73013233e-05	+1.9332	1.44639928	+1.9756
448	5.12039126e-06	+2.1921	1.06505323e-05	+2.0463	6.61947217e-06	+2.0442	1.44641443	+1.9781
896	1.32258109e-06	+1.9529	2.66836401e-06	+1.9969	1.65611553e-06	+1.9989	1.44641814	+2.0282

laplacian_dirichlet_a7.6

Mesh	\(L^\infty\) error	Order	\(L^1\) error	Order	\(L^2\) error	Order	\(\bar{T}\)	Order
38	6.85321814e-04	n/a	1.47415885e-03	n/a	9.29099092e-04	n/a	1.44728236	n/a
76	1.78344829e-04	+1.9421	3.89280922e-04	+1.9210	2.42837058e-04	+1.9358	1.44657448	n/a
152	4.31535249e-05	+2.0471	9.26095033e-05	+2.0716	5.76096928e-05	+2.0756	1.44645438	+2.5593
304	1.08057632e-05	+1.9977	2.31575043e-05	+1.9997	1.43911231e-05	+2.0011	1.44642804	+2.1889
608	2.70323392e-06	+1.9990	5.85371176e-06	+1.9841	3.63288752e-06	+1.9860	1.44642158	+2.0275
1216	6.86530963e-07	+1.9773	1.46675608e-06	+1.9967	9.08950718e-07	+1.9988	1.44641991	+1.9529

laplacian_neumann

Mesh	\(L^\infty\) error	Order	\(L^1\) error	Order	\(L^2\) error	Order	\(\bar{T}\)	Order
16	2.58282134e-02	n/a	3.02606918e-02	n/a	2.35806222e-02	n/a	1.45587136	n/a
32	8.03900539e-03	+1.6839	8.57825000e-03	+1.8187	6.68145421e-03	+1.8194	1.44858229	n/a
64	6.39003402e-03	+0.3312	8.43775609e-03	+0.0238	6.03049200e-03	+0.1479	1.44947409	n/a
128	2.86201717e-03	+1.1588	3.67657916e-03	+1.1985	2.62017001e-03	+1.2026	1.44776617	n/a
256	1.53413774e-03	+0.8996	1.95670154e-03	+0.9099	1.40162784e-03	+0.9026	1.44714474	+1.4586
512	7.56732471e-04	+1.0196	9.42623421e-04	+1.0537	6.82406659e-04	+1.0384	1.44677031	+0.7309
1024	3.64290448e-04	+1.0547	4.63361677e-04	+1.0245	3.30916762e-04	+1.0442	1.44659230	+1.0728

laplacian_neumann_o2

Mesh	\(L^\infty\) error	Order	\(L^1\) error	Order	\(L^2\) error	Order	\(\bar{T}\)	Order
16	3.90625000e-03	n/a	1.01353730e-02	n/a	6.29216185e-03	n/a	1.44068054	n/a
32	9.76562500e-04	+2.0000	2.59532267e-03	+1.9654	1.59200967e-03	+1.9827	1.44493517	n/a
64	2.44140625e-04	+2.0000	6.46928351e-04	+2.0042	3.97418535e-04	+2.0021	1.44605648	+1.9238
128	6.10351564e-05	+2.0000	1.62569143e-04	+1.9926	9.96114103e-05	+1.9963	1.44632731	+2.0497
256	1.52587896e-05	+2.0000	4.07185779e-05	+1.9973	2.49262151e-05	+1.9986	1.44639685	+1.9615
512	3.81469976e-06	+2.0000	1.01879034e-05	+1.9988	6.23408200e-06	+1.9994	1.44641369	+2.0459
1024	9.53683218e-07	+2.0000	2.54790828e-06	+1.9995	1.55880886e-06	+1.9997	1.44641796	+1.9803

laplacian_dirichlet_inverted

Mesh	\(L^\infty\) error	Order	\(L^1\) error	Order	\(L^2\) error	Order	\(\bar{T}\)	Order
16	3.70747973e-03	n/a	3.83619059e-03	n/a	3.40415006e-03	n/a	1.10328408	n/a
32	8.77206261e-04	+2.0795	6.97621489e-04	+2.4592	6.27287853e-04	+2.4401	1.10526386	n/a
64	2.54751120e-04	+1.7838	2.01567825e-04	+1.7912	1.77866611e-04	+1.8183	1.10554963	+2.7924
128	6.35717785e-05	+2.0026	4.59185072e-05	+2.1341	4.04883645e-05	+2.1352	1.10560690	+2.3190
256	1.68112807e-05	+1.9190	1.28454905e-05	+1.8378	1.13039541e-05	+1.8407	1.10561854	+2.2989
512	4.36050288e-06	+1.9469	3.10613959e-06	+2.0481	2.73405345e-06	+2.0477	1.10562359	+1.2034
1024	1.07571365e-06	+2.0192	7.49340226e-07	+2.0514	6.59091258e-07	+2.0525	1.10562468	+2.2129