1D cell stationary advection diffusion schemes

Verification of 1D cell stationary advection diffusion schemes.

Verification of 1D cell stationary advection diffusion schemes.

This test case assesses the spatial convergence of the 1D stationary advection-diffusion equation with Dirichlet boundary conditions on left and right boundaries.

Objectives

This case aims to:

1. Validate the discretization of the advection and diffusion terms in a steady advection/diffusion (scalar) equation;
2. Validate the treatment of Dirichlet and Neumann/Periodic boundary conditions;
3. Assess the spatial accuracy of second- and fourth-order schemes for moderate and extreme Péclet numbers.

Configurations

The domain is the unit square in \([0,1]^2\).
We solve the stationary advection-diffusion equation:

\[ - \nu \Delta T + \mathbf{u} \cdot \nabla T = f \]

with null right-hand-side (i.e. \( f = 0 \)). The velocity is 1D and constant, \( \mathbf{u} = (u_x, 0) \), and the diffusion coefficient \( \nu = u_x/\mathrm{Pe} \), where the Péclet number is defined as:

\[ \mathrm{Pe} = \frac{u_x L}{\nu}. \]

Since the problem is 1D in the x-direction, we expect the solution to be invariant in y.

Given Dirichlet boundary conditions on left and right, the associated exact solution is:

\[ \frac{T(x)-T_{\mathrm{left}}}{T_{\mathrm{right}} - T_{\mathrm{left}}} = \frac{e^{\frac{x \mathrm{Pe}}{L}} -1 }{e^{\mathrm{Pe}} -1}. \]

Accuracy and oscillation

We define the mesh Péclet number:

\[ \mathrm{Pe}_h = \frac{u_x h}{\nu} \]

which reduces as the mesh is refined. That number is important for the study of the numerical solution's accuracy and stability.

Illustration

Figure 1: Solution for various Péclet numbers

Boundary Conditions

Boundary	Condition	Value
left	Dirichlet	\( T = 1 \)
right	Dirichlet	\( T = 0 \)
top & bottom	Neumann or Periodic	homogeneous ( \( \partial_y T = 0 \))

Runtime Parameters

• The stationary energy equation is solved (enable_temporal_term false).
• The source term is set to zero.
• The numerical schemes are Implicit Euler with second (diffusion_scheme implicit o2_centered) or fourth (diffusion_scheme implicit o4_centered) spatial order with a star stencil.
• The boundary conditions are handled with second or third order schemes: boundary_condition_scheme quadratic or boundary_condition_scheme cubic.

Test cases

• Two cases are tested for \(\mathrm{Pe} = 1\):
  • second-order centered scheme with quadratic boundary extrapolation,
  • fourth-order centered scheme with cubic boundary extrapolation.
• For \(\mathrm{Pe} \gg 1\) and \(\mathrm{Pe} \ll 1\): fourth-order centered scheme with cubic boundary extrapolation.

The test cases can be run with the file test_cases/verification/cell_advection_diffusion_schemes/1d/energy/adv_diff_stationary.nts.

Comments

• The convergence analysis is carried out by computing errors in L1, L2, and Linf norms.
• For extreme cases, where the solution can degenerate, the behavior of schemes changes depending on the Pe number.

---

Results

Summary

• For \( 10^{-2} \leq Pe \leq 10^{2} \):
  • Second-order centered scheme with quadratic boundary extrapolation gives third-order convergence.
  • Fourth-order centered scheme with cubic boundary extrapolation gives fourth-order convergence.
  • High-order convergence observed, depending on the accuracy of boundary extrapolation scheme;
• The global accuracy is limited by the lowest-order scheme, especially the treatment of boundary conditions.
• Pe ≪ 1: saturation effect observed — the method reaches machine precision due to the simplicity of the solution;
• Pe ≫ 1: instability occurs — oscillations appear, motivating the use of upwind or TVD methods.

---

Case 1: moderate Péclet number — Pe = 1

Second-order centered scheme with quadratic BC

diffusion_scheme implicit o2_centered | o4_centered;
advection_scheme implicit o2_centered | o4_centered | houc3;
boundary_condition_scheme cubic;

This graph confirms second, third and fourth-order convergence for different combinaisons of schemes, given a fourth-order cubic boundary condition scheme.

Figure 2: Convergence graph

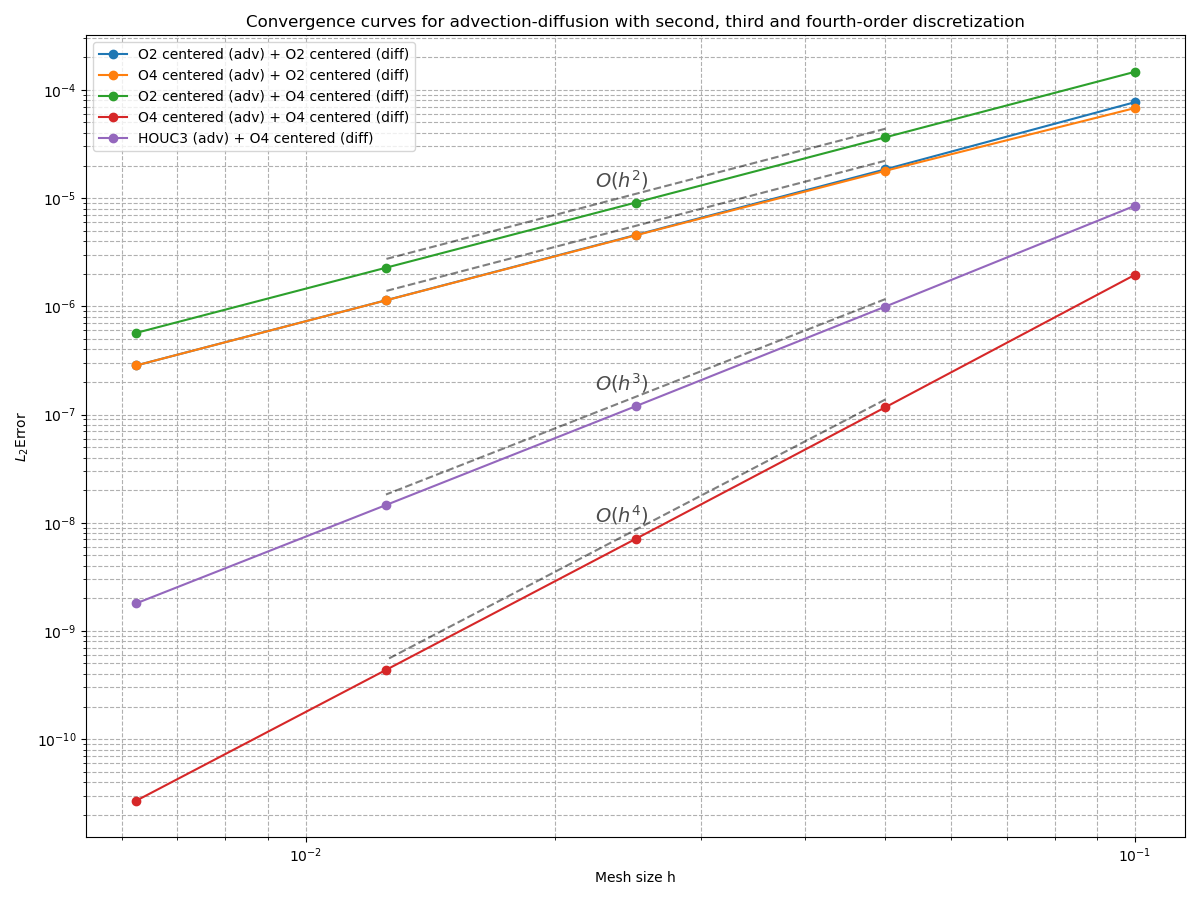
Note: Expected convergence orders are generally observed when the Péclet number is within the range \( 10^{-2} \leq \mathrm{Pe} \leq 10^{1} \).

---

Case 2: Diffusion-dominated regime — Pe ≪ 1

diffusion_scheme implicit o2_centered | o4_centered;
advection_scheme implicit o2_centered | o4_centered;
boundary_condition_scheme cubic;

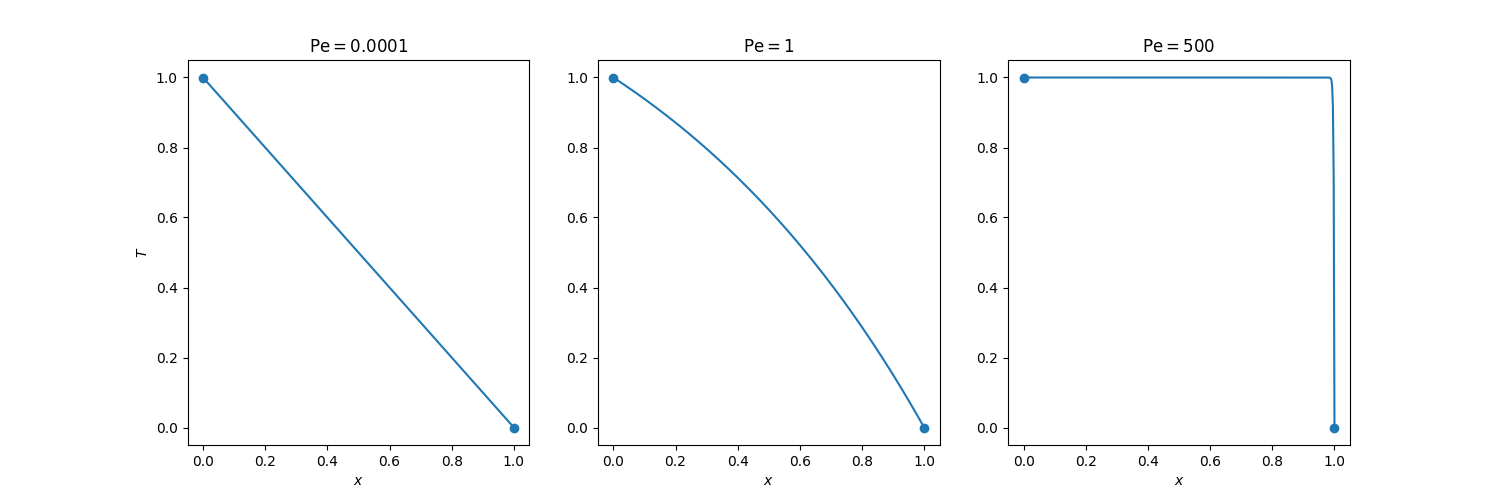
In this test, we solve the steady advection-diffusion equation with very high diffusion, i.e. \( \mathrm{Pe} = 10^{-4} \). For that case, the exact solution is very smooth and nearly affine.

Observations:

• Whatever the scheme, the error is immediately very small, close to machine precision;
• As a result, refining the mesh does not reduce the error;
• The observed behavior corresponds to numerical saturation: approximating a linear function with a high-degree polynomial introduces no additional error.

Convergence table — Second-order scheme for advection and diffusion, Pe ≪ 1

Mesh	Temperature \( L_1 \) error	order	Temperature \( L_2 \) error	order	Temperature \( L_{\infty} \) error	order
10×10	3.076298937809696e-13	n/a	3.992327850393273e-13	n/a	8.648082250317657e-13	n/a
20×20	4.0958402468260767e-13	-0.413	4.894999418797806e-13	-0.294	9.443557047461582e-13	-0.127
40×40	3.31803614531806e-13	0.304	4.057242171008019e-13	0.271	9.171552406428418e-13	0.042
80×80	3.583580905164393e-13	-0.111	4.2951250006921456e-13	-0.082	9.712022852603752e-13	-0.083
160×160	3.0775601287023584e-13	0.220	3.9487576338533454e-13	0.121	1.1652900866465643e-12	-0.263

Convergence table — Fourth-order scheme for advection and diffusion, Pe ≪ 1

Mesh	Temperature \( L_1 \) error	order	Temperature \( L_2 \) error	order	Temperature \( L_{\infty} \) error	order
10×10	3.0441878184905843e-13	n/a	3.97507249654718e-13	n/a	8.701928067011977e-13	n/a
20×20	4.115876996863e-13	-0.435	4.921520868821791e-13	-0.308	9.541256673628595e-13	-0.133
40×40	3.344625206132267e-13	0.299	4.103052387958695e-13	0.262	9.10715947100016e-13	0.067
80×80	3.474891129505962e-13	-0.055	4.1671838393714256e-13	-0.022	9.700747150009903e-13	-0.091
160×160	2.8254159467716893e-13	0.299	3.6662711714813503e-13	0.185	9.992145999504487e-13	-0.043

Conclusion

No meaningful convergence can be deduced. The numerical solution reaches a plateau due to limited machine precision.
The solution is practically a straight line — fitting it with a 4th-order polynomial yields negligible residuals.

---

Case 3: Advection-dominated regime — Pe ≫ 1

diffusion_scheme implicit o4_centered;
advection_scheme implicit o1_upwind | o2_upwind | o2_centered | houc3 | o4_centered;
boundary_condition_scheme cubic;

In this section, we investigate the numerical behavior of the advection–diffusion equation for a high Péclet number (Pe = 500), where the advection term dominates. The solution is quite sharp, because of superior advection, and challenges the numerical schemes.

Diffusion is discretized using a 4th-order centered scheme, while boundary conditions are handled with a cubic scheme. Only the advection scheme is varied in order to compare accuracy and possible oscillations.

Convergence

The tables in the appendix show convergence rates associated to the the advection scheme (from 1 to 4), as expected. Be careful that, at Péclet number larger than 2, oscillations may alter the convergence rate. We thus chose to start the mesh convergence at \( \mathrm{Pe} = 3.125 \).

Positivity preservation

The min/max conservation of the solution is, ideally, expected. Depending on the scheme, we observe oscillations (near the right boundary) due to the numerical properties of the advection-diffusion coupling, depending on the mesh Péclet number. Oscillations can be proven to appear for \(\mathrm{Pe}_h \ge 2\) with the second-order centered schemes and can be tackled with the use of an upwind advection scheme, as for example with the first order scheme. Moreover, boundary schemes have influence as they are coupled with the advection-diffusion schemes. Figure 3 illustrates the min/max values for every couple of schemes.

Figure 3: Converegence graph of min/max values

Comments

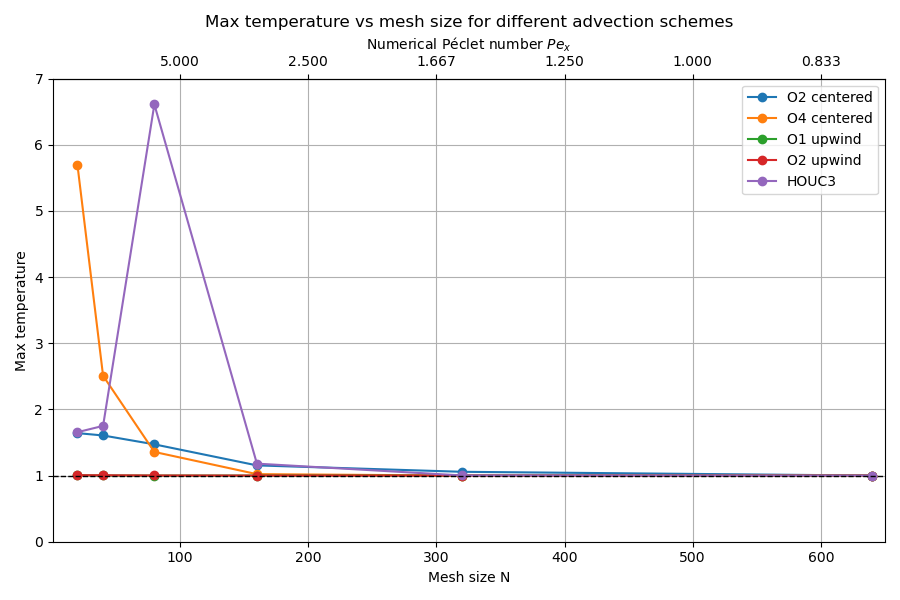
The convergence study of the maximum and minimum values for various advection schemes shows the following trends:

• Maximum values:
  • O1 upwind and O2 upwind remain close to the expected physical bound (≈ 1), with O1 being the most stable and monotone scheme.
  • O2 centered and HOUC3 sometimes show overshoots above 1, which is a typical behavior of higher-order advection schemes when combined with insufficient numerical diffusion.
  • O4 centered produces very large spurious oscillations for coarse meshes (N = 10, 20, 40), but converges correctly when the mesh is refined (N ≥ 80).
  • The numerical Péclet number (Pe = 500/N) indicates that for high Pe (coarse meshes), oscillations dominate in high-order schemes, while for small Pe (fine meshes), accuracy improves and values remain bounded.

In summary, low-order upwind schemes provide stability but at the cost of accuracy, whereas higher-order centered schemes achieve better convergence but are highly sensitive to the mesh size and the numerical Péclet number.

Conclusion

Centered schemes show important oscillations in this regime. A more stable upwind scheme should be preferred when \(\mathrm{Pe}_h \gg 2\).

Annexe

Case 1: moderate Péclet number — Pe = 1

Advection O2 centered + diffusion O2 centered + cubic

Mesh	Temperature \( L_1 \) error	order	Temperature \( L_2 \) error	order	Temperature \( L_{\infty} \) error	order
10×10	7.110313317222103e-05	n/a	7.709319716524254e-05	n/a	1.049915200799223e-04	n/a
20×20	1.6841227668907578e-05	2.078	1.8455978215433737e-05	2.063	2.5470315403008925e-05	2.043
40×40	4.151369355808782e-06	2.020	4.562944018403443e-06	2.016	6.311104322143102e-06	2.013
80×80	1.034136265615827e-06	2.005	1.1375325758807836e-06	2.004	1.5743330975537262e-06	2.003
160×160	2.5830174347907765e-07	2.001	2.8418239883512675e-07	2.001	3.933474835848827e-07	2.001

Advection O4 centered + diffusion O2 centered + cubic

Mesh	Temperature \( L_1 \) error	order	Temperature \( L_2 \) error	order	Temperature \( L_{\infty} \) error	order
10×10	6.1297299113537e-05	n/a	6.801444014405986e-05	n/a	9.512071508899211e-05	n/a
20×20	1.6223701542502303e-05	1.918	1.788546553923447e-05	1.927	2.4833514004063417e-05	1.937
40×40	4.112602358413217e-06	1.980	4.527143592391392e-06	1.982	6.270596994872868e-06	1.986
80×80	1.0317074436703357e-06	1.995	1.1352895867341748e-06	1.996	1.5718092443162135e-06	1.996
160×160	2.5814952917317504e-07	1.999	2.840417874558925e-07	1.999	3.9318873235050233e-07	1.999

Advection O2 centered + diffusion O4 centered + cubic

Mesh	Temperature \( L_1 \) error	order	Temperature \( L_2 \) error	order	Temperature \( L_{\infty} \) error	order
10×10	1.3467017749612927e-04	n/a	1.4710428667780387e-04	n/a	2.0241173992319172e-04	n/a
20×20	3.320520595429137e-05	2.020	3.6470054569953545e-05	2.012	5.045437517980922e-05	2.004
40×40	8.27268254514762e-06	2.005	9.09823485012667e-06	2.003	1.2591330352362817e-05	2.003
80×80	2.0663862222483234e-06	2.001	2.273334533247571e-06	2.001	3.146745152227126e-06	2.000
160×160	5.164850566319967e-07	2.000	5.682562402794638e-07	2.000	7.865738679280199e-07	2.000

Advection O4 centered + diffusion O4 centered + cubic

Mesh	Temperature \( L_1 \) error	order	Temperature \( L_2 \)error	order	Temperature \( L_{\infty} \) error	order
10×10	1.8283083294221013e-06	n/a	1.9581343939158866e-06	n/a	3.633710309910998e-06	n/a
20×20	1.0946009252247798e-07	4.062	1.1670760024008423e-07	4.069	2.3877613297002e-07	3.928
40×40	6.6902440714754375e-09	4.032	7.0867924923823664e-09	4.042	1.5314548611894407e-08	3.963
80×80	4.133900781313605e-10	4.016	4.35838628830309e-10	4.023	9.698106467198597e-10	3.981
160×160	2.564579322882323e-11	4.011	2.697445263744445e-11	4.014	6.10157957145474e-11	3.990

Case 3: Advection-dominated regime — Pe >> 1

• Diffusion scheme: O4 centered
• Boundary scheme: cubic

O2 centered

N	Pe = 500/N	Max temperature	order	Temperature L1 error	order	Temperature L2 error	order	Temperature Linf error	order
160×4	3.125	1.153764989873273	n/a	0.032740481289562244	n/a	0.39693025446553204	n/a	5.018211188769706	n/a
320×8	1.5625	1.0569369335830208	n/a	0.0014606197102087213	4.486	0.016879794190739393	4.556	0.24988288858223895	4.328
640×16	0.7813	1.0000000000001505	0.766	0.00024063105670532294	2.602	0.002692066861112279	2.649	0.04371007887532541	2.515
1280×32	0.3906	0.999999999999995	38.413	5.339634677626918e-05	2.172	0.0005965366762243941	2.174	0.00984772635872444	2.150
2560×64	0.1953	0.9999999999999953	nan	1.2887116115095763e-05	2.051	0.00014405486720236158	2.050	0.0023667574359877985	2.057
5120×128	0.09765	0.9999999999999923	nan	3.190197134465769e-06	2.014	3.5666225899604904e-05	2.014	0.0005868121054873887	2.012

O4 centered

N	Pe = 500/N	Max temperature	order	Temperature L1 error	order	Temperature L2 error	order	Temperature Linf error	order
160×4	3.125	1.0215671867893708	n/a	0.0021579702242837625	n/a	0.017135833479726734	n/a	0.16077199660757047	n/a
320×8	1.5625	1.0000000000000209	n/a	0.0001833965602015934	3.557	0.0019305815968240065	3.150	0.02815433401854961	2.514
640×16	0.7813	1.00000000000019	nan	1.2656857257610122e-05	3.857	0.00016530245969005461	3.546	0.003733454536263281	2.915
1280×32	0.3906	0.9999999999999953	nan	7.995941841933956e-07	3.985	1.1551299562067275e-05	3.839	0.0003625962949609096	3.364
2560×64	0.1953	0.9999999999999953	nan	4.852058923825658e-08	4.043	7.188203201799841e-07	4.006	2.8785365959432818e-05	3.655
5120×128	0.09765	0.9999999999999927	nan	2.9636024146894595e-09	4.033	4.295639857669098e-08	4.065	2.0373293133507664e-06	3.821

O1 upwind

N	Pe = 500/N	Max temperature	order	Temperature L1 error	order	Temperature L2 error	order	Temperature Linf error	order
160×4	3.125	1.000000000000024	n/a	0.00178407958547918	n/a	0.015611966454890555	n/a	0.17699202627548793	n/a
320×8	1.5625	1.0000000000000393	n/a	0.0011144526700285226	0.679	0.010590010479147571	0.560	0.12694170297612772	0.480
640×16	0.7813	1.0000000000002187	-3.550	0.0006421739058642161	0.795	0.006556698384443601	0.692	0.10025786391570257	0.340
1280×32	0.3906	0.9999999999999952	nan	0.0003500898079776607	0.875	0.003734129018085411	0.812	0.05858256434996889	0.775
2560×64	0.1953	0.9999999999999947	8.653	0.00018411528695549324	0.927	0.002009794417375664	0.894	0.03232944085819922	0.858
5120×128	0.09765	0.9999999999999941	-0.000	9.468619749833585e-05	0.959	0.0010459173378449525	0.942	0.017008866182353866	0.927

O2 upwind

N	Pe = 500/N	Max temperature	order	Temperature L1 error	order	Temperature L2 error	order	Temperature Linf error	order
160×4	3.125	1.0000032957168814	n/a	0.0009178047177706905	n/a	0.008561817070250147	n/a	0.10011305907094714	n/a
320×8	1.5625	1.0000000000000253	n/a	0.0004995970894534595	0.877	0.0050073749466989495	0.774	0.060430663902330206	0.728
640×16	0.7813	1.0000000000002325	nan	0.0002142985298368106	1.221	0.002290881862251645	1.128	0.03683366807404387	0.714
1280×32	0.3906	0.9999999999999919	nan	7.373808539021602e-05	1.539	0.0008125205277880098	1.495	0.013232087355502187	1.477
2560×64	0.1953	0.9999999999999931	nan	2.1747303890842297e-05	1.762	0.00024213227991520732	1.747	0.003965313163662443	1.739
5120×128	0.09765	0.9999999999999918	nan	5.891604471912937e-06	1.884	6.57966525788961e-05	1.880	0.0010814264548021368	1.874

HOUC3

N	Pe = 500/N	Max temperature	order	Temperature L1 error	order	Temperature L2 error	order	Temperature Linf error	order
160×4	3.125	1.1802836813843247	n/a	0.0038358234052973477	n/a	0.039640885324899636	n/a	0.4861195619445483	n/a
320×8	1.5625	1.0016855083081044	n/a	0.0005094592900704622	2.912	0.005462929672300457	2.859	0.07667184179685149	2.665
640×16	0.7813	1.0000000000001312	6.727	7.122433546815692e-05	2.839	0.0007795536076492235	2.809	0.012011844350684475	2.674
1280×32	0.3906	0.999999999999994	33.516	9.500482137198837e-06	2.906	0.00010531033467621856	2.888	0.0017097491033888357	2.813
2560×64	0.1953	0.9999999999999951	nan	1.220801894038357e-06	2.960	1.3609706676876384e-05	2.952	0.00022249583055145017	2.942
5120×128	0.09765	0.9999999999999921	nan	1.5420170009300998e-07	2.985	1.7224268147333265e-06	2.982	2.8305948745921405e-05	2.975