Laplacian test cases with Neumann boundary conditions (2D/3D)

This test case solves the 2D/3D Laplace equation with Neumann - homogeneous or not - boundary conditions on all boundaries. The aims of this test case are:

1. validate the discretization of the diffusive term of a cell advection/diffusion equation
2. validate Neumann boundary conditions

Configurations

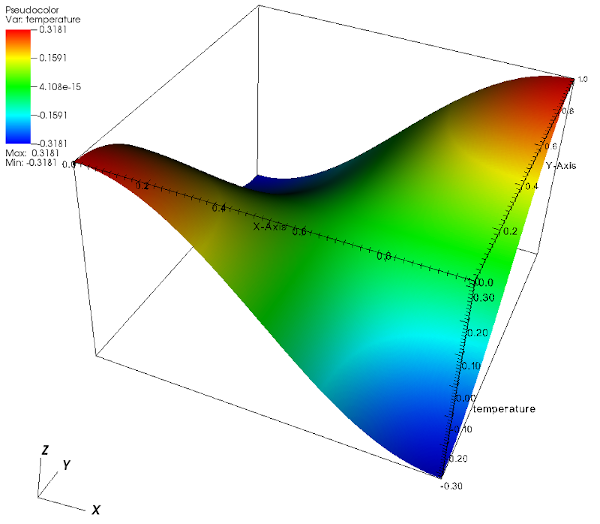
Domain is rectangular, its opposite corner coordinates being \((0,0,0)\) and \((1,1,1)\). We solve \(- \Delta T=f\) on the whole domain. Neumann - homogeneous or not - boundary conditions are applied all boundaries. The \(\alpha\) parameter helps to switch from homogeneous ( \(\alpha = 0\)) to non homogeneous case ( \(\alpha = 1\)). Reference solutions of the probem in 2D/3D are (see figure below):

• \( cos(\pi x + \alpha)\ cos(\pi y + \alpha)\ /\ \pi \)
• \( cos(\pi x + \alpha)\ cos(\pi y + \alpha) cos(\pi z + \alpha)\ /\ \pi \)

Right-end-side in 2D/3D are:

• \( 2 \pi \cos(\pi x + \alpha)\ cos(\pi y + \alpha)\ /\ \pi \)
• \( 3 \pi \cos(\pi x + \alpha)\ cos(\pi y + \alpha)\ cos(\pi z + \alpha)\ /\ \pi \)

Figure 1: Elevation of the 2D temperature field in the non homogeneous case

Runtime parameters

Energy equation is used:

• temporal and inertial terms are disabled;
• Hypre solvers are used;
• \( \alpha = 1 \)

Comments

Second order spatial convergence is expected.

Results

The grid size starts from 10 in every direction to 160. Second order convergence is observed with \(L_2\), \(L_1\) or \(L_\infty\) norms.

2D results

3D results