Laplacian test cases with Dirichlet boundary conditions in the 2D axisymmetric coordinate system.

Laplacian test cases with Dirichlet boundary conditions in the 2D axisymmetric coordinate system.

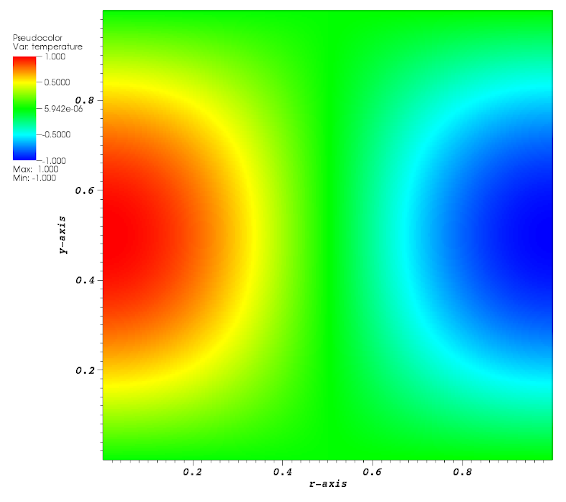
The aim of this test case is to validate the discretization of the diffusive term of a cell advection/diffusion equation in the 2D axisymmetric coordinate system.

Configurations

Domain is rectangular, its opposite corner coordinates being \((0,0)\) and \((1,1)\).

We solve \(-\Delta T=f\) on the whole domain.

Using cylindrical coordinates, 2D solution of the problem is set to \(\cos(\pi r)\sin(\pi y)\). Right-end-side f is equal to \(2\pi^{2}\cos(\pi r)\sin(\pi y) + \dfrac{\pi}{r}\sin(\pi r)\sin(\pi y)\).

Boundary condition

The symmetry axis is in located on the left at \( r=0.5 \). The global boundary conditions are chosen as follows.

Figure 1: Elevation of the temperature field

Runtime parameters

Energy equation is used:

• the temporal and advection term are not solved;
• MUMPS or HYPRE solvers can be used.

Comments

Second order spatial convergence is expected.

Results

The grid size starts from 40 in every direction to 640. Second order convergence is observed with \(L_\infty\), \(L_1\) or \(L_2\) norms.

2D results