Thermosolutal natural convection in a square/cubic cavity.

This test cases simulate the thermosolutal natural convection problem in a cubic cavity following the work of I. Sezai and A. A. Mohamad [1] on double diffusive convection in a cubic enclosure with opposing temperature and concentration gradients.

validate the discretization of the Navier-Stokes equations with regular (or not) grids;
validate the discretization of the energy equation and species transport equations;
validate the coupling between these equations thanks to the Boussinesq approximation.

Configurations

Two configurations are chosen: a 2D one, \( Ra=10^7 \), \( Le=1 \) and \( Pr=0.71 \); a 3D one \( Ra=10^5 \), \( Le=10 \). For both the ratio between the buoyancy forces \( N=-0.2 \). Flows are laminar and stationary. Domain is square/cubic, its opposite corner coordinates being \((0,0,0)\) and \((1,1,1)\). We solve the Navier-Stokes, the energy and species equations equations on the whole domain in their nondimensional forms. Boussinesq approximation is done, density varies linearly with temperature and concentration, and the driving pressure is considered. All boundaries are considered as adiabatic wall boundaries, except the left and right ones where opposite temperature and concentration of 1 and 0, respectively, are set.

Runtime parameters

To better approximate the boundary layers attached to the wall boundaries, a refined mesh closed to the wall is used. Centered scheme is used for Navier-Stokes equation as well as for the diffusion term of the transport equations. For the convective term of the scalar transport equations, first, second order upwind and QUICK schemes are compared.

Comments

To check the symmetry of the code, a rotation of the configuration is tested and produces same results up to computer precision. This done in the validation script of the code.

Results

2D case

Temperature field and streamlines of the velocity feld, obtained with a 320x320 grid, are presented figure 1 and 2.

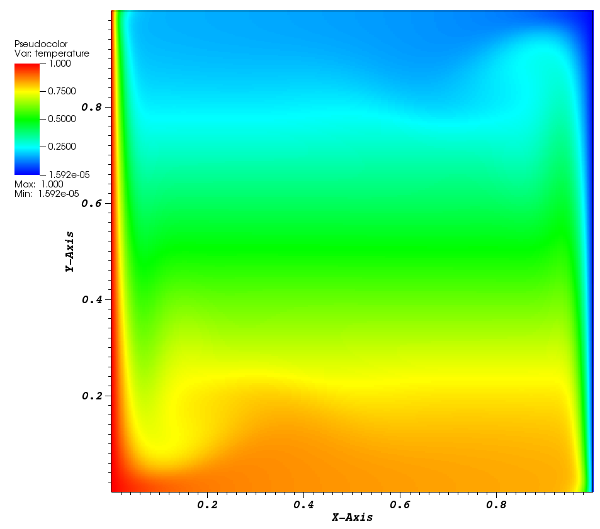
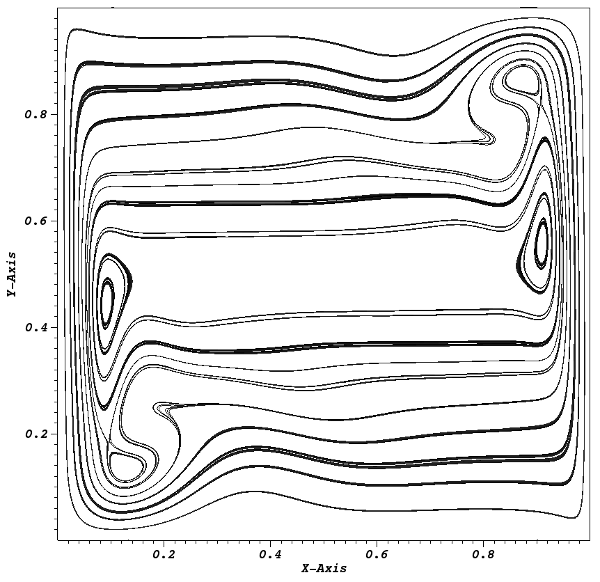
Nusselt number is closed to the ones observed in literature, 13.53 and 13.6 in [1] and [2], respectively. First order convergence is observed on Nusselt number for first order upwind scheme:

Mesh	Left Nusselt	Order
40	13,97998950
80	13,84654926
160	13,78077542	1.02
320	13,74946080	1.07
extrapolated	13,72100382

Second order convergence is observed on Nusselt number for second order upwind and QUICK schemes:

Mesh	Left Nusselt	Order
40	13,8375084
80	13,7519877
160	13,7280073	1.83
320	13,7219985	1.99
extrapolated	13,7199895

Mesh	Left Nusselt	Order
40	13,7557972
80	13,7308452
160	13,7228953	1.65
320	13,7207594	1.89
640	13.7202125	1.96
extrapolated	13.7199748

3D case

Next figures show the 3D structures of the flow as well as isocontour of temperature and concentrations, on the mid XY plane, in accordance with [1]. Nusselt number Nu=4.43 and Sherwood number Sh=10.71 are also in agreement with [1].

References

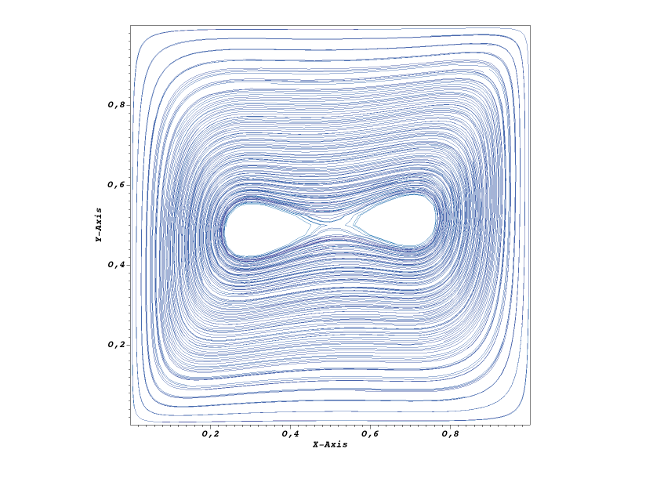
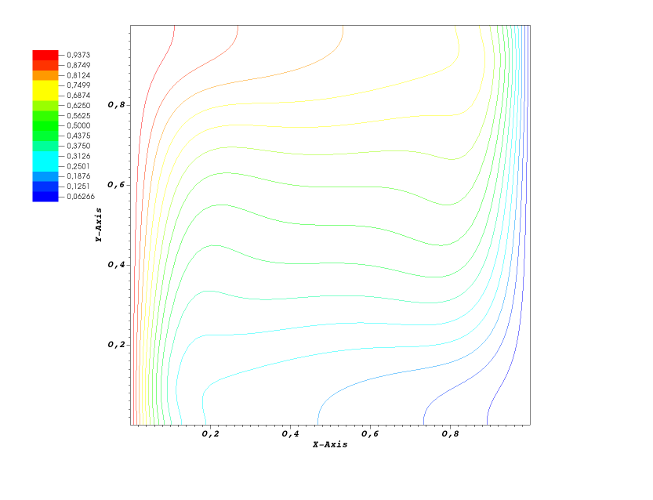
[1] Sezai, and A. A. Mohamad, Double diffusive convection in a cubic enclosure with opposing temperature and concentration gradients, Physics of Fluids 12, 2210 (2000).

[2] C. Beghein, F. Haghighat, and F. Allard, Numerical study of double-diffusive natural convection in a square cavity, Int. J. Heat Mass Transf. 35, 833, 1992.