This page will help you choose among the various advection schemes available for Notus. The following point of views and advices are given in the context of the available code and implemented numerical methods. Thus, they should not be taken as a generality. However, they represent a discerning guide for most of the applications that can be simulated with Notus.

We first give a quick overview of the available numerical schemes for the pure advection equation. Then, we go further in details by considering the advection-diffusion equation shared by most physical models.

Pure advection

Equation

The advection equation of a scalar variable \( \phi \), in its primitive form, is:

\[ \frac{\partial \phi}{\partial t} + \mathbf{u} \cdot \nabla \phi = 0 \]

where \( \mathbf{u} \) is the velocity of the flow. In a conservative form – as it is common in a Finite Volume approach –, the pure advection equation is rewritten:

\[ \frac{\partial \phi}{\partial t} + \nabla \cdot \left( \mathbf{u} \phi \right) = \phi \nabla \cdot \mathbf{u} \]

which can be simplified when considering an incompressible flow with \( \nabla \cdot \mathbf{u} = 0 \).

Various numerical schemes (see below) are available in Notus and may be chosen in the NTS file.

Numerical schemes

There are two main categories of schemes for solving the advection equation in Notus:

Implicit schemes: stable but low to moderate order in space
Explicit schemes: conditionally stable but higher order

Note: Implicit advections schemes will permit to avoid the CFL restriction. On the other hand, one should consider their relative diffusivity (first order upwind) and oscillation property (see the Reynolds/Péclet number below for the second order centered scheme) compared to explicit schemes. We refer the reader to the (future) CFL best practice for more discussion on this topic.; Higher order implicit schemes can be implemented. However, they usualy have a higher computational cost as for their wider stencil. For now, in Notus, only the second order centered and upwind implicit schemes are implemented.

Implicit schemes

See also: Cell advection term for more mathematical and implementation details on implicit schemes for the advection equation.

There are 3 classical implicit spatial schemes:

First order upwind: o1_upwind
Second order upwind: o2_upwind
Second order centered: o2_centered

plus two hybrid schemes for the Navier equation:

Hybrid first order: hybrid_o2_centered_o1_upwind
Hybrid second order: hybrid_o2_centered_o2_upwind

The first three ones are tested in the verification/cell_advection_schemes/species_1D/species_linear_advection_1D_implicit test case, which consist of the classical 1D pure advection with constant velocity. Here is visual result of the advection of an initial exponential function after 100 time steps: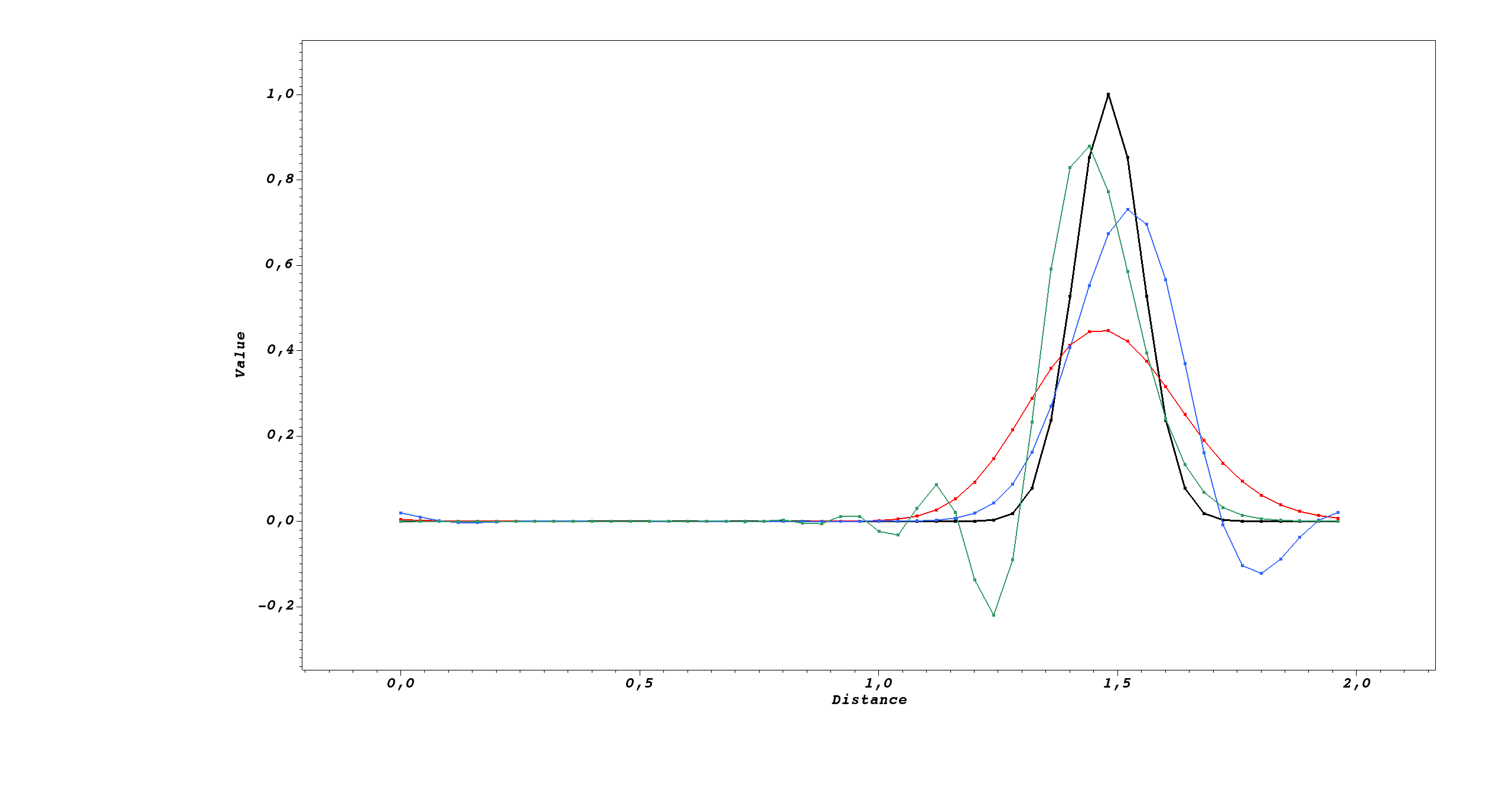

One can clearly notice the main particularities of the various schemes:

Remember

Scheme	Damping	Dephasing	Other
First order upwind	High (-60%)	No	–
Second order upwind	Moderate (-25%)	Forward	Upfront negative values
Second order centered	Moderate (-15%)	Backward	Trailing oscillations with negative values

Important: When considering the second order upwind scheme, one has to keep in mind that the matrix' stencils become larger as we need to incorporate points at a greater distance. The performance of the solver will thus be impacted, inducing longer computationnal time and more memory usage.

The following figure shows the impact of temporal precision by comparison between first order in time (SBDF1) and second order in time (SBDF2) schemes: 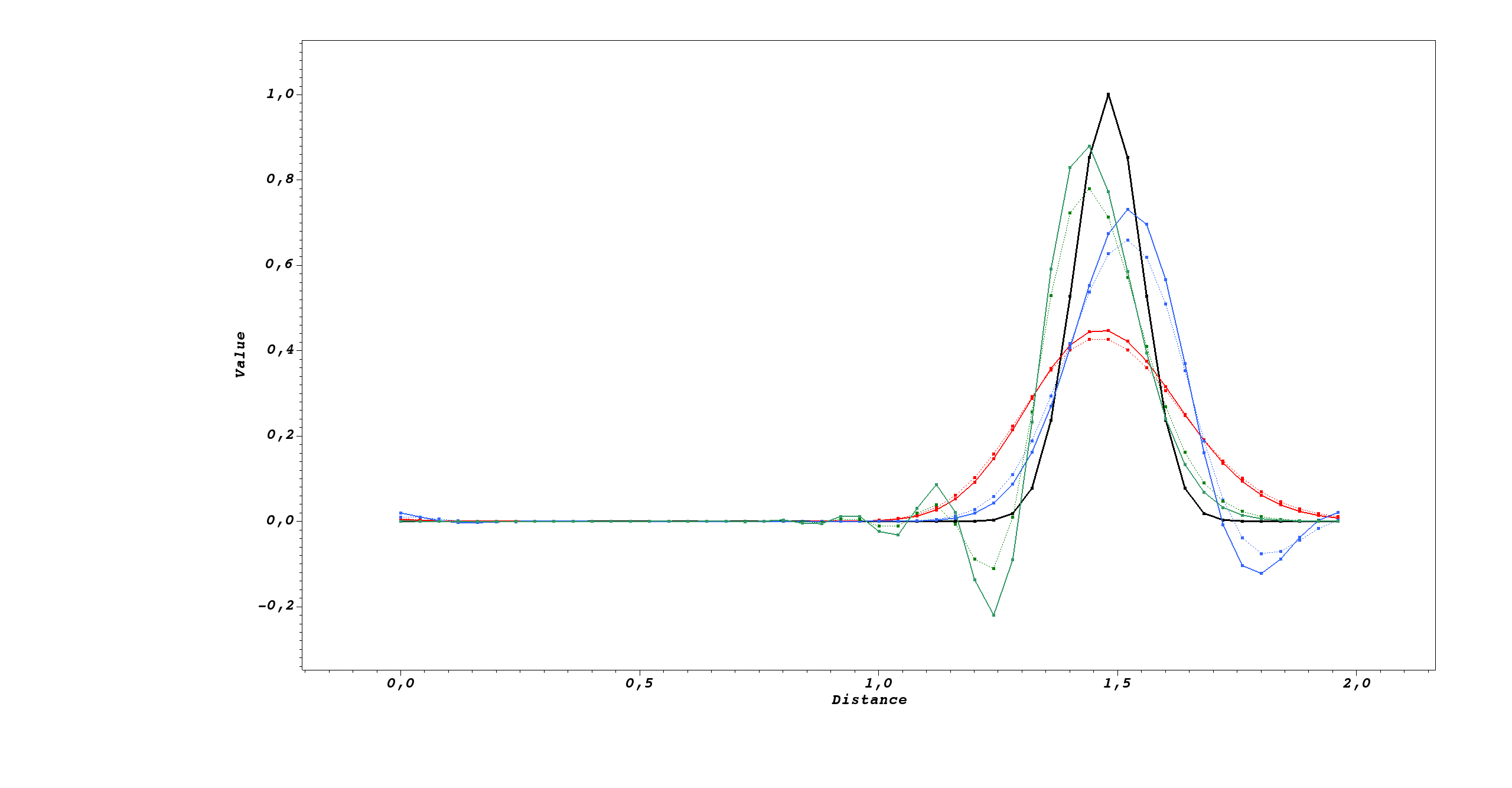Hence, SBDF2 is clearly less diffusive than SBDF1 with a loss of around 10% for SBDF1/SBDF2.

See also: Discretization of PDE for more information about SBDF temporal schemes

Explicit schemes

See also: Cell scalar advection for more mathematical and implementation details on explicit schemes for the advection equation

There are 2 classical explicit spatial schemes:

First order upwind: o1_upwind
Second order upwind: o2_upwind

plus two high-order WENO schemes:

WENO 3,2 upwind: weno3
WENO 5,3 upwind: weno5

Note: WENO N,M schemes are at best order N (with smooth fields) and at worse order M (with discontinuous fields). The Z family of WENO schemes is more precise than the classical one. For more information, please refer to the associated WENO documentation in the code.

The 4 different schemes are tested in the verification/cell_advection_schemes/species_1D/species_linear_advection_1D_explicit test case, which consist of the classical 1D pure advection with constant velocity (as in implicit). However, it is important to note that here, for stability criterions for the high-order schemes, a second order RK scheme NSSP32 have been used for all schemes. Here is visual result of the advection of an initial exponential function after 100 time steps: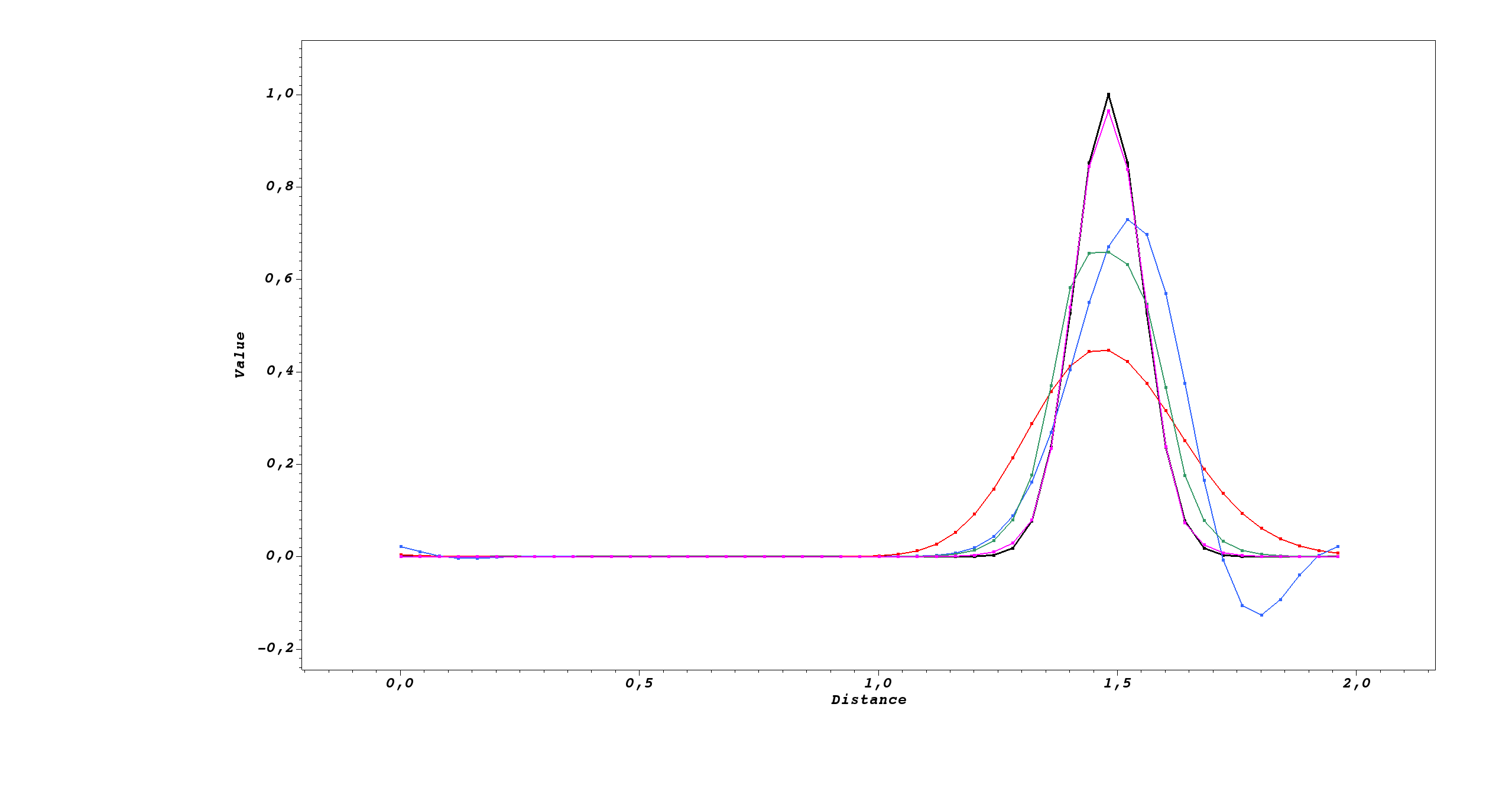

One can clearly notice the main particularities of the various schemes:

Remember

Scheme	Damping	Dephasing	Other
First order upwind	High (-60%)	No	Superposed with the equivalent implicit scheme
Second order upwind	Moderate (-25%)	Forward	Negative values + Superposed with the equivalent implicit scheme
WENO 3,2 upwind	Moderate (-33%)	Slightly backward	No discernible (but existing) negative values
WENO 5,3 upwind	Low (-2.5%)	Not discernible	No discernible (but existing) negative values

Important: Explicit advection schemes have particular internal temporal integration schemes based on Runge-Kutta methods (see Cell scalar advection for more information). Hence, for the pure advection problem, using SBDF1 or SBDF2 with an explicit second order (at least) scheme like NSSP32 will always be second order in time. However, when coupled with a diffusion equation, it is important to use the SBDF2 scheme to achieve 2nd order for the advection-diffusion equation.

Note: WENO schemes do not impose a constraint on the positivity of the solution nor its upper bound (even though they manage to reach very low error). Thus, one cannot rely on such properties that can be attain through adequate limiters or post-processing of the advected quantity.

Advection-diffusion

We now consider the more complex problem of solving an advection-diffusion equation. Different choices can be made depending on the relative importance of the two terms. In this section we recall common knowledge on the advection-diffusion equation treatment and provide hints on how to choose the appropriate numerical scheme for the advection term.

Know your physics

First of all, one should always look at the dimensionless numbers of the physical problem that you are simulating. Also, in numerical simulation, one has to account for the effective cell dimensionless number which shows the relative importance between two terms of an equation at the cell scale.

Cell Reynolds number

This is particularly important for the inertia and viscous terms (eq. to advection and diffusion) of the Navier-Stokes equation, for which the associated cell Reynolds number \( Re_{cell} = \frac{\rho_{cell} |u_{cell}| \delta x}{\mu_{cell}} \) shows the relative importance between advection and diffusion of the flow. For the energy (resp. species) equation, the cell Péclet (resp. Schmidt) number plays a similar role. For the sake of clarity, we will focus on the Reynolds number.

If the cell Reynolds number is approximately equal to 1, it means that, at the scale of a cell, the diffusion term and the advection term are of the same order of magnitude. Below unity, diffusion starts to dominate numerically (see slow advection below); above that, advection starts to dominate numerically (see fast advection below).

Note: It is quite noticeable that, the more you refine the discretization of your domain (ie. the smallest the cells), the lower the cell Reynolds number. At the cell scale, this means that the viscous term becomes more and more dominant and, from a numerical point of view, this term should be considered with more care.

Important: While \( Re_{cell} \rightarrow 0 \) as \( \delta x \rightarrow 0 \), this does not imply that the advection/inertial term becomes negligeable at the physical scale of the simulation when refining the grid! The inertial term has, of course, still to be computed as it contributes to the large scale phenomena. Inertia can be neglected if and only if the overall Reynolds number is sufficiently small at the studied phenomena's scale. A similar argument holds in the other extramum.

The knowledge of the (approximate/maximum/minimum) value of the cell Reynolds number will give you hints on the choice of an adequate numerical scheme for the advection term. For example, for slow advection problems, it might be unefficient and unecessary to use high-order explicit schemes such as WENO. In that case, a classical fast second order centered implicit scheme might be very sufficient!

Slow advection

For low cell Reynolds numbers, \( Re_{cell} \ll 1 \), the advection/inertial/transport term is not dominant. Hence, the impact of numerical errors in this term on the whole simulation will also be negligeable. Thus, an implicit scheme will be a good choice toattain low computational time and large time steps.

It is well known that, for \( Re_{cell} < 2 \), a second order centered implicit scheme can be used. Above that, the scheme will become oscillating and an upwind implicit or explicit scheme should be considered. The choice of a first order upwind scheme will permit to numerically damp high frequencies while not being dephasing at all, ie. all the waves will travel at the good speed but will see their energy decrease. Unless using appropriate flux limiters, the second order upwind scheme might bring unwanted over/undershoots in the solution (numerical values above or below the physical limits), this is why we prefer WENO explicit schemes in such cases (see next section).

Note: The later over/undershoot problem should be avoided / treated when considering the advection of energy, volume fraction, etc. as, for example, a negative value of the volume fraction is non physical.

Anyway, a second order SBDF method should be used to reduce the impact of important temporal error when choosing a large time step.

Fast advection

For large cell Reynolds numbers, \( Re_{cell} \gg 1 \), the advection/inertial/transport term becomes dominant. Hence, the impact of numerical errors in this term will be very important on the whole simulation. Thus, low order schemes should be avoided and high-order explicit schemes – like WENO – favorized. However, be careful that high-order schemes can get very computationally consuming, particularly the WENO 5,3 scheme that has to be used with (at least) a NSSP 3,2 2nd order in time integration scheme (see the next paragraph for a discussion about accuracy vs efficiency).

Warning: If, somehow, you have to deal with a discontinuity somewhere in the field that you are advecting, even though WENO schemes are made to adapt to discontinuities, lower order schemes should be prefered – even localy – in order to avoid to propagate more errors. See the (future) dealing with discontinuities best practice page.

Finding the good balance: accuracy vs efficiency

Example: Consider the advection-diffusion problem where the local cell Reynolds number is \( Re_{cell,1} = 8 \) with a very coarse mesh of size \( \delta x_{1} \) and adequate time step \( \delta t_{1} \) at CFL number \(\sigma_1=1\). An explicit WENO 3,2 scheme should be sufficient.
If now one wants to divide the mesh by \(2^4=16\), this would lead to \( \delta x_{2} = \delta x_{1} / 16 \), thus \( Re_{cell,2} = Re_{cell,1}/16 = 0.5 \). With the same unity CFL number, the time step will also be reduced to \( \delta t_{2} = \delta t_{1} / 16 \).

As at cells' scale viscosity becomes dominant, we might relax the need for accuracy in the advection equation and favorize a low order implicit scheme, and at the same time increase the CFL number to \( \sigma_2 = 4 \).

Hence, while we have a total number of cells multiplied by \(16^2=256\), using a first order implicit scheme for the advection will reduce the computational time per iteration (cost divided by ~4) and, coupled with an increased CFL number (cost divided by ~4), this choice will drastically reduce the total computational time compared to an explicit scheme, while not reducing much the overall accuracy. We can thus expect a total gain of 1600% in computational time when comparing an explicit and implicit treatment of the advection equation for a reasonnable loss in precision.

Warning: When increasing the CFL number, time errors will undoubtfully increase and high-order temporal schemes like at least the SBDF2 should be used.