Test Backward facing step flow.

coordinate with immersed boundaries.

These test cases study laminar axisymmetric through confined annular geometries with backward facing step modeled by immersed boundaries. The axisymmetric steady ﬂow of an incompressible Newtonian ﬂuid is solved in the \((r,y)\) plane. The dependence of reattachment length on Reynolds number ranging from 50 to 400 is presented and compared with the experiments and numerical solutions ([1], [2], [3]).

Configurations

The geometry is constructed based on the reference case [1] but in vertical direction, as shown in Fig.1.

Figure 1: Step cylinder geometry.

The boundary conditions for the system are

\(u = 0, v = 0 \) at the right and immersed boundaries,
\(u = 0, \frac{\partial{v}}{\partial{r}} = 0\) at the left axis of symmetry,
\(u = 0, v = 2 u_{mean} \left[1-\left(\frac{r}{R}\right)\right]^2\) at the bottom and
\(u = 0, \frac{\partial{v}}{\partial{y}} = 0\) at the top.

Runtime parameters

Navier-Stokes equation is used with HYPRE or MUMPS solvers.

Results

Figure 2: Axisymmetric flow over a backward-facing step at Re=200: streamlines and vertical velocity field.

Mesh	mean_pressure	Order	mean_velocity_u	Order	mean_velocity_v	Order	mean_velocity_magnitude	Order
64	-8.83402351e-02	n/a	5.02550612e-03	n/a	5.38946479e-01	n/a	5.49199039e-01	n/a
128	-8.99617909e-02	n/a	5.01111985e-03	n/a	5.40406307e-01	n/a	5.50865946e-01	n/a
256	-9.08452280e-02	+0.8762	5.00330500e-03	+0.8804	5.41229619e-01	+0.8263	5.51819015e-01	+0.8065
512	-9.13076517e-02	+0.9339	4.99928058e-03	+0.9574	5.41667023e-01	+0.9125	5.52328508e-01	+0.9035

In the validation of the code, the nondimensionalized reattachment length \(L_{H}\) is almost linear for Reynolds number range covered by the study with various expansion ratio \(\beta\).

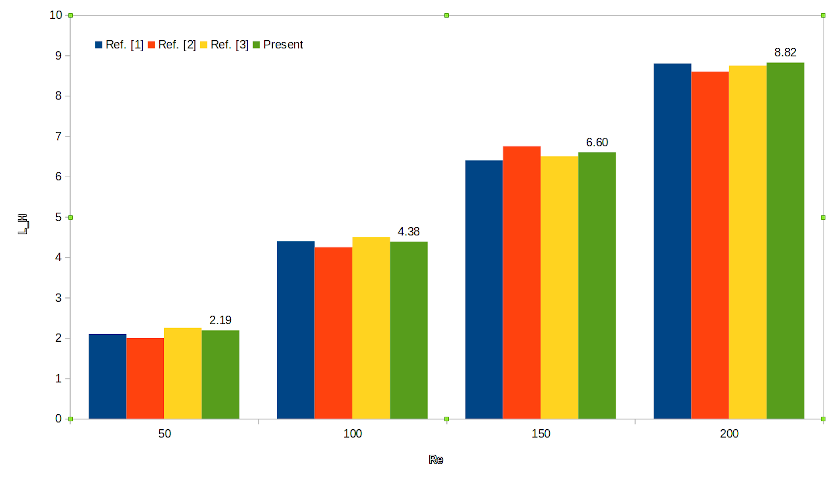
Figure 3: Comparions of the reattachment length for Re=100 and expansion ratio equal to 2.

References

[1] Hammad, K., Ötügen, M. & Arik, A PIV study of the laminar axisymmetric sudden expansion flow, E. Experiments in Fluids (1999) 26: 266.

[2] Macagno EO; Hung TK, Computational and experimental study of a captive eddy, J Fluid Mech (1967) 28: 43—64.

[3] Dağtekin İ, Ünsal M. Numerical analysis of axisymmetric and planar sudden expansion flows for laminar regime, Int J Numer Methods Fluids (2011) 65: 1133–44.