Validation of the 3D Poiseuille Rayleigh Benard flow.

Configurations

In [1] and [2], a solution to a benchmark problem for a three-dimensional mixed convection flow in a horizontal rectangular channel heated from below and cooled from above (Poiseuille-Rayleigh-Bénard flow) has been proposed. This flow is a steady thermoconvective longitudinal roll flow in a large aspect ratio channel at moderate Reynolds and Rayleigh numbers (Re=50, Ra=5000) (Reynolds number,Rayleigh number) and Prandtl number Pr=0.7 (Prandtl number). The model is based on the non dimensional Navier-Stokes equations with Boussinesq approximation. In the present validation exercise, we compare Notus solution to the different solutions of [1].

A 2D "Poiseuille" flow is imposed at the channel entrance and the incoming fluid is cold, at temperature \( Tc=0 \). After an entrance zone over which a zero heat flux is imposed on the four walls, the top horizontal wall is maintained at the cold temperature \( Tc \) and the bottom wall is maintained at a higher temperature \( Th=1 \). The vertical lateral walls are adiabatic. Full description is done in [1] pdf. The resulting flow pattern is the ten longitudinal roll steady flow. It is symmetrical with respect to the median longitudinal vertical plane and can therefore be computed on half of the domain.

Runtime parameters

Centered second order advection scheme is used for the Navier-Stokes equations and the Energy one.

Stationary tolerance is set to \( 10^{-11} \).

To converge quicker to the stationary solution, time step of the Energy equation is set 1000 thousand times higher than the Navier-Stokes one.

Simulation is done with a symmetry front boundary condition.

Comments

Very few solver iterations are set to converge quicker to the stationary solution. Residuals are quite high at the beginning, but are reduced little by littel as the time iterations increase.

Results

Next figures show temperature field on the horizontal mid-plane and on the right boundary, and velocity vector and temperature on a vertical plane plane at \( x=30 \) that exhibits the 5 longitudinal rolls.

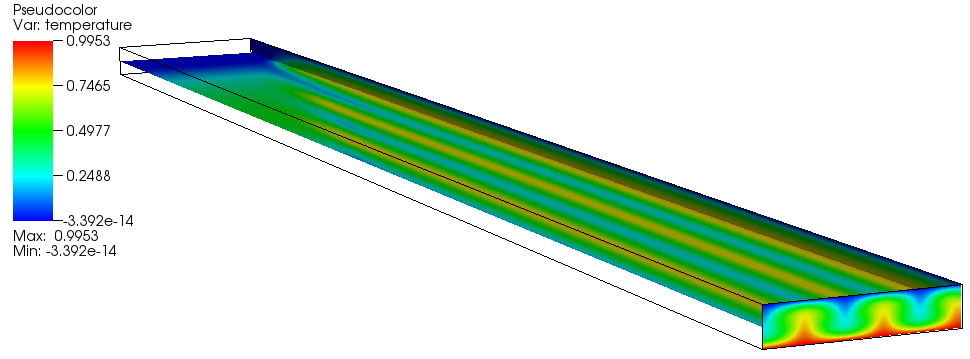
Figure 1: Temperature field on the horizontal mid-plane and on the right boundary.

Figure 2: Velocity vector and temperature field on a vertical plane at x=30.

We first compare (see next Table) the mean quantities computed in [1]: the mean temperature, the mean kinetic energy and the mean pressure gradient.

Mesh	Mean temperature	Mean kinetic energy	Mean pressure difference
600x40x160	0.448400	0.646096	14.38841
900x60x240	0.448466	0.646164	14.39622
1350x90x360	0.448511	0.646196	14.40001
Order	0.94	1.86	1.30
Extrapolated	0.448560	0.646209	14.40293
Reference Solution [1]	0.448604	0.646227	14.40670

Next we compare Nusselt numbers, heat and momentum fluxes through the channel faces (TODO).

References

[1] Xavier Nicolas, Marc Medale, Stéphane Glockner, Stéphane Gounand, Benchmark Solution for a Three-Dimensional Mixed-Convection Flow, Part 1: Reference Solutions, Numerical Heat Transfer Part B-fundamentals, vol. 60, no. 5, pp. 325-345, 2011 pdf.

[2] Xavier Nicolas, Stéphane Gounand, Marc Medale, Stéphane Glockner, Benchmark Solution for a Three-Dimensional Mixed-Convection Flow, Part 2: Analysis of Richardson Extrapolation in the Presence of a Singularity, Numerical Heat Transfer Part B-fundamentals, vol. 60, no. 5, pp. 346-369, 2011 pdf.