Variables associated with domain partitioning context. More...

Variables
integer	rank = 0
	Rank for the current local domain (associated to an MPI process).

type(mpi_comm)	mpi_comm_notus
	Notus MPI communicator (Cartesian aware). This variable is initialized to mpi_comm_world in the early stage of Notus initialization?

Numbers of local domains.
Total number of local domains.
integer	n_mpi_proc = 1

integer	n_mpi_proc_x = 1
	Number of local domains along the x-axis.

integer	n_mpi_proc_y = 1
	Number of local domains along the y-axis.

integer	n_mpi_proc_z = 1
	Number of local domains along the z-axis.

integer, dimension(:), allocatable	proc_direction
	Values `n_mpi_proc_x, n_mpi_proc_y, n_mpi_proc_z` stored in an array.

integer, dimension(:), allocatable	proc_coordinate
	Coordinates of the current local domain in the Cartesian processor grid.

logical	is_repartitioning = .false.
	Will the domain be repartitioned?

logical	is_repartitioning_achieved = .false.
	Has the repartitioning process been already achieved?

logical	is_initial_step_repartitioning = .true.
	Is it the initial step in the repartitioning process? If so, stop the calculation and print the required number of processors.

integer	n_cells_proc = 0
	Number of cells per partition.

integer	label_wanted_partitioning = -1
	Label of the wanted partitioning.

Neighborhood information.
Domain ranks for the six neighbors. The value `-1` means “no neighbor.” Give the rank of any domain from its relative coordinates.
integer, dimension(:,:,:), allocatable	neighbor_proc

integer, dimension(:), allocatable	neighbor_proc_list
	Give the list of the neighboring processors in the repartitioning process.

integer, dimension(:,:), allocatable	neighbor_points_list
	Give the start and end indices of the points to exchange between neighbor processors.

logical	mpi_exchange_full = .true.
	MPI exchange including corners (and edges in 3D)

integer	n_exchange_proc = -1
	Number of neighbor domains to communicate with.

Processor information with respect to boundaries.
False or true depending whether they are at a physical boundary or not Is the processor on the left boundary of the domain
logical	is_proc_on_left_boundary = .false.

logical	is_proc_on_right_boundary = .false.
	Is the processor on the right boundary of the domain.

logical	is_proc_on_bottom_boundary = .false.
	Is the processor on the bottom boundary of the domain.

logical	is_proc_on_top_boundary = .false.
	Is the processor on the top boundary of the domain.

logical	is_proc_on_back_boundary = .false.
	Is the processor on the back boundary of the domain.

logical	is_proc_on_front_boundary = .false.
	Is the processor on the front boundary of the domain.

Periodic information (location of the periodic boundary)
These variables are set ONLY IF there are more than one proc in the given direction. Example 1: 'is_proc_on_left_periodic == .false.' if 'is_periodic_x == .true.' and 'n_mpi_proc_x == 1'. Example 2: 'is_proc_on_left_periodic == .true.' if 'is_periodic_x == .true.' and 'n_mpi_proc_x > 1' and 'is_proc_on_left_boundary'.
logical	is_proc_on_left_periodic = .false.

logical	is_proc_on_right_periodic = .false.

logical	is_proc_on_top_periodic = .false.

logical	is_proc_on_bottom_periodic = .false.

logical	is_proc_on_back_periodic = .false.

logical	is_proc_on_front_periodic = .false.

Local domain start and end indices in the physical domain (with no ghost cells)
indexing.
integer	is_global_physical_domain = 1

integer	is_global_physical_domain_r = 1

integer	is_global_physical_domain_t = 1

integer	js_global_physical_domain = 1

integer	js_global_physical_domain_r = 1

integer	js_global_physical_domain_t = 1

integer	ks_global_physical_domain = 1

integer	ks_global_physical_domain_r = 1

integer	ks_global_physical_domain_t = 1

integer	ie_global_physical_domain = 1

integer	ie_global_physical_domain_r = 1

integer	ie_global_physical_domain_t = 1

integer	je_global_physical_domain = 1

integer	je_global_physical_domain_r = 1

integer	je_global_physical_domain_t = 1

integer	ke_global_physical_domain = 1

integer	ke_global_physical_domain_r = 1

integer	ke_global_physical_domain_t = 1

integer	isu_global_physical_domain = 1

integer	ieu_global_physical_domain = 1

integer	jsv_global_physical_domain = 1

integer	jev_global_physical_domain = 1

integer	ksw_global_physical_domain = 1

integer	kew_global_physical_domain = 1

Local domain start and end indices in the overlapping numerical domain (with boundary and overlapping boundary cells)
indexing.
integer	is_global_overlap_numerical_domain = 1

integer	is_global_overlap_numerical_domain_r = 1

integer	is_global_overlap_numerical_domain_t = 1

integer	js_global_overlap_numerical_domain = 1

integer	js_global_overlap_numerical_domain_r = 1

integer	js_global_overlap_numerical_domain_t = 1

integer	ks_global_overlap_numerical_domain = 1

integer	ks_global_overlap_numerical_domain_r = 1

integer	ks_global_overlap_numerical_domain_t = 1

integer	ie_global_overlap_numerical_domain = 1

integer	ie_global_overlap_numerical_domain_r = 1

integer	ie_global_overlap_numerical_domain_t = 1

integer	je_global_overlap_numerical_domain = 1

integer	je_global_overlap_numerical_domain_r = 1

integer	je_global_overlap_numerical_domain_t = 1

integer	ke_global_overlap_numerical_domain = 1

integer	ke_global_overlap_numerical_domain_r = 1

integer	ke_global_overlap_numerical_domain_t = 1

Coordinates of the left, bottom, back corner.
double precision, dimension(:), allocatable	global_domain_corners1_x

double precision, dimension(:), allocatable	global_domain_corners1_y

double precision, dimension(:), allocatable, target	global_domain_corners1_z

double precision, dimension(:), allocatable	global_domain_corners2_x
	Coordinates of the right, top, front corner.

double precision, dimension(:), allocatable	global_domain_corners2_y

double precision, dimension(:), allocatable, target	global_domain_corners2_z

List of all partition sizes.
The arrays starts at zero en ends on n_mpi_proc_-1. E.g.: `global_domain_list_n(0:n_mpi_proc_*-1)`
integer, dimension(:), allocatable	global_domain_list_nx

integer, dimension(:), allocatable	global_domain_list_nx_r

integer, dimension(:), allocatable	global_domain_list_nx_t

integer, dimension(:), allocatable	global_domain_list_ny

integer, dimension(:), allocatable	global_domain_list_ny_r

integer, dimension(:), allocatable	global_domain_list_ny_t

integer, dimension(:), allocatable	global_domain_list_nz

integer, dimension(:), allocatable	global_domain_list_nz_r

integer, dimension(:), allocatable	global_domain_list_nz_t

List of the starting indices of the faces of all partitions.
The arrays starts at zero en ends on n_mpi_proc_-1. E.g.: `global_domain_list_s(0:n_mpi_proc_-1)`
integer, dimension(:), allocatable	global_domain_list_isu

integer, dimension(:), allocatable	global_domain_list_isu_r

integer, dimension(:), allocatable	global_domain_list_isu_t

integer, dimension(:), allocatable	global_domain_list_jsv

integer, dimension(:), allocatable	global_domain_list_jsv_r

integer, dimension(:), allocatable	global_domain_list_jsv_t

integer, dimension(:), allocatable	global_domain_list_ksw

integer, dimension(:), allocatable	global_domain_list_ksw_r

integer, dimension(:), allocatable	global_domain_list_ksw_t

List of the ending indices of the faces of all partitions.
The arrays starts at zero en ends on n_mpi_proc_-1. E.g.: `global_domain_list_e(0:n_mpi_proc_-1)`
integer, dimension(:), allocatable	global_domain_list_ieu

integer, dimension(:), allocatable	global_domain_list_ieu_r

integer, dimension(:), allocatable	global_domain_list_ieu_t

integer, dimension(:), allocatable	global_domain_list_jev

integer, dimension(:), allocatable	global_domain_list_jev_r

integer, dimension(:), allocatable	global_domain_list_jev_t

integer, dimension(:), allocatable	global_domain_list_kew

integer, dimension(:), allocatable	global_domain_list_kew_r

integer, dimension(:), allocatable	global_domain_list_kew_t

Detailed Description

Variables associated with domain partitioning context.

The global domain is partitioned in a Cartesian arrangement of local domains, as described in computational_domain. The numbers of local domain per direction are n_mpi_proc_x, n_mpi_proc_y, and n_mpi_proc_z, and the total number local domains is n_mpi_proc = prox_nb_x × n_mpi_proc_y × n_mpi_proc_z. Each local domain is identified by its coordinates proc_coordinate in the partitioning system, and also by its rank. Both coordinates and ranks ranges from 0 to some n-1.

Figure 1: Local domain indexing.

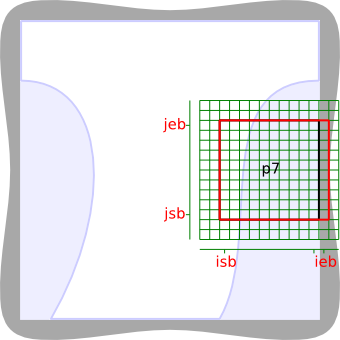
The module variables are defined within the context of a local domain (SIMD paradigm); they are distributed or local variables. Although, some variables have the same value for each local domain, thus can be considered as a shared or global variable.

Global numerical domain.

As described in computational_domain, the mesh is indexed locally over an extended domain, the numerical domain. It is sometimes necessary to define a global indexing.

Refined grid (under development): grid can be globally refined for phase advection. Suffix _r is associated to the refined grids, suffix _t is associated to the temporary grid.

Variable Documentation

◆ global_domain_corners1_x

double precision, dimension(:), allocatable variables_mpi::global_domain_corners1_x

◆ global_domain_corners1_y

double precision, dimension(:), allocatable variables_mpi::global_domain_corners1_y

◆ global_domain_corners1_z

double precision, dimension(:), allocatable, target variables_mpi::global_domain_corners1_z

◆ global_domain_corners2_x

double precision, dimension(:), allocatable variables_mpi::global_domain_corners2_x

Coordinates of the right, top, front corner.

◆ global_domain_corners2_y

double precision, dimension(:), allocatable variables_mpi::global_domain_corners2_y

◆ global_domain_corners2_z

double precision, dimension(:), allocatable, target variables_mpi::global_domain_corners2_z

◆ global_domain_list_ieu

integer, dimension(:), allocatable variables_mpi::global_domain_list_ieu

◆ global_domain_list_ieu_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_ieu_r

◆ global_domain_list_ieu_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_ieu_t

◆ global_domain_list_isu

integer, dimension(:), allocatable variables_mpi::global_domain_list_isu

◆ global_domain_list_isu_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_isu_r

◆ global_domain_list_isu_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_isu_t

◆ global_domain_list_jev

integer, dimension(:), allocatable variables_mpi::global_domain_list_jev

◆ global_domain_list_jev_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_jev_r

◆ global_domain_list_jev_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_jev_t

◆ global_domain_list_jsv

integer, dimension(:), allocatable variables_mpi::global_domain_list_jsv

◆ global_domain_list_jsv_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_jsv_r

◆ global_domain_list_jsv_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_jsv_t

◆ global_domain_list_kew

integer, dimension(:), allocatable variables_mpi::global_domain_list_kew

◆ global_domain_list_kew_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_kew_r

◆ global_domain_list_kew_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_kew_t

◆ global_domain_list_ksw

integer, dimension(:), allocatable variables_mpi::global_domain_list_ksw

◆ global_domain_list_ksw_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_ksw_r

◆ global_domain_list_ksw_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_ksw_t

◆ global_domain_list_nx

integer, dimension(:), allocatable variables_mpi::global_domain_list_nx

◆ global_domain_list_nx_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_nx_r

◆ global_domain_list_nx_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_nx_t

◆ global_domain_list_ny

integer, dimension(:), allocatable variables_mpi::global_domain_list_ny

◆ global_domain_list_ny_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_ny_r

◆ global_domain_list_ny_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_ny_t

◆ global_domain_list_nz

integer, dimension(:), allocatable variables_mpi::global_domain_list_nz

◆ global_domain_list_nz_r

integer, dimension(:), allocatable variables_mpi::global_domain_list_nz_r

◆ global_domain_list_nz_t

integer, dimension(:), allocatable variables_mpi::global_domain_list_nz_t

◆ ie_global_overlap_numerical_domain

integer variables_mpi::ie_global_overlap_numerical_domain = 1

◆ ie_global_overlap_numerical_domain_r

integer variables_mpi::ie_global_overlap_numerical_domain_r = 1

◆ ie_global_overlap_numerical_domain_t

integer variables_mpi::ie_global_overlap_numerical_domain_t = 1

◆ ie_global_physical_domain

integer variables_mpi::ie_global_physical_domain = 1

◆ ie_global_physical_domain_r

integer variables_mpi::ie_global_physical_domain_r = 1

◆ ie_global_physical_domain_t

integer variables_mpi::ie_global_physical_domain_t = 1

◆ ieu_global_physical_domain

integer variables_mpi::ieu_global_physical_domain = 1

◆ is_global_overlap_numerical_domain

integer variables_mpi::is_global_overlap_numerical_domain = 1

◆ is_global_overlap_numerical_domain_r

integer variables_mpi::is_global_overlap_numerical_domain_r = 1

◆ is_global_overlap_numerical_domain_t

integer variables_mpi::is_global_overlap_numerical_domain_t = 1

◆ is_global_physical_domain

integer variables_mpi::is_global_physical_domain = 1

◆ is_global_physical_domain_r

integer variables_mpi::is_global_physical_domain_r = 1

◆ is_global_physical_domain_t

integer variables_mpi::is_global_physical_domain_t = 1

◆ is_initial_step_repartitioning

logical variables_mpi::is_initial_step_repartitioning = .true.

Is it the initial step in the repartitioning process? If so, stop the calculation and print the required number of processors.

◆ is_proc_on_back_boundary

logical variables_mpi::is_proc_on_back_boundary = .false.

Is the processor on the back boundary of the domain.

◆ is_proc_on_back_periodic

logical variables_mpi::is_proc_on_back_periodic = .false.

◆ is_proc_on_bottom_boundary

logical variables_mpi::is_proc_on_bottom_boundary = .false.

Is the processor on the bottom boundary of the domain.

◆ is_proc_on_bottom_periodic

logical variables_mpi::is_proc_on_bottom_periodic = .false.

◆ is_proc_on_front_boundary

logical variables_mpi::is_proc_on_front_boundary = .false.

Is the processor on the front boundary of the domain.

◆ is_proc_on_front_periodic

logical variables_mpi::is_proc_on_front_periodic = .false.

◆ is_proc_on_left_boundary

logical variables_mpi::is_proc_on_left_boundary = .false.

◆ is_proc_on_left_periodic

logical variables_mpi::is_proc_on_left_periodic = .false.

◆ is_proc_on_right_boundary

logical variables_mpi::is_proc_on_right_boundary = .false.

Is the processor on the right boundary of the domain.

◆ is_proc_on_right_periodic

logical variables_mpi::is_proc_on_right_periodic = .false.

◆ is_proc_on_top_boundary

logical variables_mpi::is_proc_on_top_boundary = .false.

Is the processor on the top boundary of the domain.

◆ is_proc_on_top_periodic

logical variables_mpi::is_proc_on_top_periodic = .false.

◆ is_repartitioning

logical variables_mpi::is_repartitioning = .false.

Will the domain be repartitioned?

◆ is_repartitioning_achieved

logical variables_mpi::is_repartitioning_achieved = .false.

Has the repartitioning process been already achieved?

◆ isu_global_physical_domain

integer variables_mpi::isu_global_physical_domain = 1

◆ je_global_overlap_numerical_domain

integer variables_mpi::je_global_overlap_numerical_domain = 1

◆ je_global_overlap_numerical_domain_r

integer variables_mpi::je_global_overlap_numerical_domain_r = 1

◆ je_global_overlap_numerical_domain_t

integer variables_mpi::je_global_overlap_numerical_domain_t = 1

◆ je_global_physical_domain

integer variables_mpi::je_global_physical_domain = 1

◆ je_global_physical_domain_r

integer variables_mpi::je_global_physical_domain_r = 1

◆ je_global_physical_domain_t

integer variables_mpi::je_global_physical_domain_t = 1

◆ jev_global_physical_domain

integer variables_mpi::jev_global_physical_domain = 1

◆ js_global_overlap_numerical_domain

integer variables_mpi::js_global_overlap_numerical_domain = 1

◆ js_global_overlap_numerical_domain_r

integer variables_mpi::js_global_overlap_numerical_domain_r = 1

◆ js_global_overlap_numerical_domain_t

integer variables_mpi::js_global_overlap_numerical_domain_t = 1

◆ js_global_physical_domain

integer variables_mpi::js_global_physical_domain = 1

◆ js_global_physical_domain_r

integer variables_mpi::js_global_physical_domain_r = 1

◆ js_global_physical_domain_t

integer variables_mpi::js_global_physical_domain_t = 1

◆ jsv_global_physical_domain

integer variables_mpi::jsv_global_physical_domain = 1

◆ ke_global_overlap_numerical_domain

integer variables_mpi::ke_global_overlap_numerical_domain = 1

◆ ke_global_overlap_numerical_domain_r

integer variables_mpi::ke_global_overlap_numerical_domain_r = 1

◆ ke_global_overlap_numerical_domain_t

integer variables_mpi::ke_global_overlap_numerical_domain_t = 1

◆ ke_global_physical_domain

integer variables_mpi::ke_global_physical_domain = 1

◆ ke_global_physical_domain_r

integer variables_mpi::ke_global_physical_domain_r = 1

◆ ke_global_physical_domain_t

integer variables_mpi::ke_global_physical_domain_t = 1

◆ kew_global_physical_domain

integer variables_mpi::kew_global_physical_domain = 1

◆ ks_global_overlap_numerical_domain

integer variables_mpi::ks_global_overlap_numerical_domain = 1

◆ ks_global_overlap_numerical_domain_r

integer variables_mpi::ks_global_overlap_numerical_domain_r = 1

◆ ks_global_overlap_numerical_domain_t

integer variables_mpi::ks_global_overlap_numerical_domain_t = 1

◆ ks_global_physical_domain

integer variables_mpi::ks_global_physical_domain = 1

◆ ks_global_physical_domain_r

integer variables_mpi::ks_global_physical_domain_r = 1

◆ ks_global_physical_domain_t

integer variables_mpi::ks_global_physical_domain_t = 1

◆ ksw_global_physical_domain

integer variables_mpi::ksw_global_physical_domain = 1

◆ label_wanted_partitioning

integer variables_mpi::label_wanted_partitioning = -1

Label of the wanted partitioning.

◆ mpi_comm_notus

type(mpi_comm) variables_mpi::mpi_comm_notus

Notus MPI communicator (Cartesian aware). This variable is initialized to mpi_comm_world in the early stage of Notus initialization?

◆ mpi_exchange_full

logical variables_mpi::mpi_exchange_full = .true.

MPI exchange including corners (and edges in 3D)

◆ n_cells_proc

integer variables_mpi::n_cells_proc = 0

Number of cells per partition.

◆ n_exchange_proc

integer variables_mpi::n_exchange_proc = -1

Number of neighbor domains to communicate with.

◆ n_mpi_proc

integer variables_mpi::n_mpi_proc = 1

◆ n_mpi_proc_x

integer variables_mpi::n_mpi_proc_x = 1

Number of local domains along the x-axis.

◆ n_mpi_proc_y

integer variables_mpi::n_mpi_proc_y = 1

Number of local domains along the y-axis.

◆ n_mpi_proc_z

integer variables_mpi::n_mpi_proc_z = 1

Number of local domains along the z-axis.

◆ neighbor_points_list

integer, dimension(:,:), allocatable variables_mpi::neighbor_points_list

Give the start and end indices of the points to exchange between neighbor processors.

◆ neighbor_proc

integer, dimension(:,:,:), allocatable variables_mpi::neighbor_proc

◆ neighbor_proc_list

integer, dimension(:), allocatable variables_mpi::neighbor_proc_list

Give the list of the neighboring processors in the repartitioning process.

◆ proc_coordinate

integer, dimension(:), allocatable variables_mpi::proc_coordinate

Coordinates of the current local domain in the Cartesian processor grid.

◆ proc_direction

integer, dimension(:), allocatable variables_mpi::proc_direction

Values n_mpi_proc_x, n_mpi_proc_y, n_mpi_proc_z stored in an array.

◆ rank

integer variables_mpi::rank = 0

Rank for the current local domain (associated to an MPI process).