Base function to number Cartesian neighbors. More...

Functions/Subroutines
pure subroutine	mod_generate_stencil::generate_stencil (n, stl, stl_index, spatial_dimension, do_orig, do_xy_quad, do_yz_quad, do_zx_quad, naxes, nquad, nocts)
	Populate stencil index array.

integer function, dimension(3)	mod_generate_stencil::shift_stencil_loc (indices, direction)
	Shift neighbor index to match array index.

Detailed Description

The mod_generate_stencil::generate_stencil routine assigns numbers to nodes placed in a 2D or 3D Cartesian arrangements. It is the base function for building actual stencils, which are done in the mod_set_cell_stencil_indices::set_cell_stencil_indices and in the mod_set_face_stencil_indices::set_face_stencil_indices routines.

Numbering principles

Neighbor categories

The nodes around (0,0,0) are divided into the four following categories:

ORIG: the node (0,0,0),
AXES: nodes on the Cartesian axes (origin excluded),
QUAD: nodes on the Cartesian planes (Cartesian axes excluded),
OCTS: nodes on the Cartesian octants (Cartesian planes excluded).

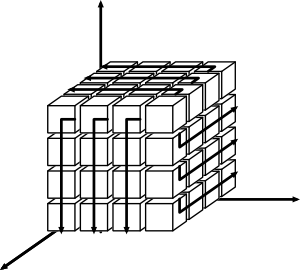
Figures 1.1 to 1.4 illustrates each category.

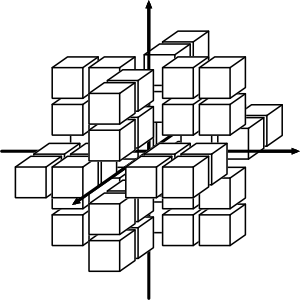
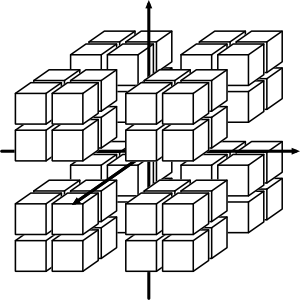
The number of nodes in each category can be found in the development of a binomial series. Considering nodes for a box of extent $ n_s $ (e.g. from $-n_s$ to $n_s$ in every axis), the total number of nodes is:

\[ n = (1 + 2 n_s)^d = \begin{cases} 1 &+& 4 n_s &+& 4 n_s^2 &+& 0 & \text{if $d = 2,$} \\ 1 &+& 6 n_s &+& 12 n_s^2 &+& 8 n_s^3 & \text{if $d = 3,$} \end{cases} \]

where each term in the development corresponds to the number of nodes in a category: ORIG, AXES, QUAD, and OCTS, respectively. There is no OCTS in 2D.

QUAD nodes.

The QUAD nodes are spread in three planes:

xy-plane,
yz-plane,
zx-plane.

In 2D, there is only one plane: xy-plane. Each plane is divided into four quarter-planes, which are identified by the orientation of their axes:

Plane:         xy    yz    zx

Quad       I: (--)  (--)  (--)
index:    II: (+-)  (+-)  (+-)
         III: (++)  (++)  (++)
          IV: (-+)  (-+)  (-+)

Examples:

  y ↑           z ↑           x ↑
 IV │ III      IV │ III      IV │ III
────┼──── →   ────┼──── →   ────┼──── →
  I │ II  x     I │ II  y     I │ II  z

OCTS nodes.

Axes:
(1st,2nd,3rd)      xyz

Oct            I: (---)
index:        II: (+--)
             III: (++-)
              IV: (-+-)
               V: (-++)
              VI: (+++)
             VII: (+-+)
            VIII: (--+)

Numbering order

Nodes in a box of extent $n_s$ are numbered continuously according to the order described below:

Number the ORIG node,
Number the AXES nodes:
- in the first direction (x-axis), number the first node on the negative side (left), then on the positive side (right),
- next, do the same in the next axes (y-axis, then z-axis if in 3D),
- repeat the two previous steps one node farther from (0,0,0), and so on until $n_s$.
Number the QUAD nodes:
- in the first sub-category (xy-plane), number the first node on the diagonal of each quadrant, according to the order given above,
- in 3D only, do the same in the next planes (yz-plane, zx-plane),
- now number the nodes from the diagonal point to the second plane axis, in the same quadrant order (see example below),
- and do the same for each points between the diagonal point and the first plane axis, again in the same quadrant order,
- repeat the five previous points one node farther from (0,0,0), and so on until $n_s$.
In 3D only, number the OCTS nodes:
- number the first node on the diagonal of each octant, according to the order given above,
- next, number the node next to the diagonal node towards the x-axis, and number the nodes from this one along the z-axis.
- repeat the last point, one node farther in the x-axis
- repeat the last two points along the y-axis and x-axis, respectively, and along the z-axis and y-axis, respectively.
- then do the same one diagonal farther from (0,0,0).

Example of quadrant III filling:

y ↑
  ┌───────────┐
  │   ┊ ← ┊ 4 │
  ├───────┐ ┈ │
  │ 2 ┊ 1 │   │
  ├───┐ ┈ │ ┈ │
  │   │ 3 │   │
  └───┴───┴───┘ →
                x

Mixed face nodes

To number mixed faces nodes, one should use the generate_stencil routine with do_orig = .false., naxes = 0, and only one plane set to true. The example below illustrates mixed numbering in the xy-plane.

The y-face nodes that surround some x-face node is most naturally and clearly numbered as follows:

    ┌───^───┬───^───┐  +½
    │       │       │
    >       >       >  0
    │       │       │
    └───^───┴───^───┘  -½

       -½   0  +½

Although, fractional indices being not handled by most computer architectures, The gen_stencil routine uses integers indices as follows:

    ┌───^───┬───^───┐  +1
    │       │       │
    >       >       >  0
    │       │       │
    └───^───┴───^───┘  -1

       -1   0  +1

Although, this indices does not matches the actual numbering of y-faces nodes. The function shift_stencil_loc translates the indices.

Notus indexing:
    ┌───^───┬───^───┐  +1
    │       │       │
    >       >       >  0
    │       │       │
    └───^───┴───^───┘  0

       -1   0   0

Hypre indexing:
    ┌───^───┬───^───┐  0
    │       │       │
    >       >       >  0
    │       │       │
    └───^───┴───^───┘  -1

        0   0  +1

Function/Subroutine Documentation

◆ generate_stencil()

pure subroutine mod_generate_stencil::generate_stencil	(	integer, intent(in)	n,
		integer, dimension(-n:n,-n:n,-n:n), intent(inout)	stl,
		integer, intent(inout)	stl_index,
		integer, intent(in)	spatial_dimension,
		logical, intent(in)	do_orig,
		logical, intent(in)	do_xy_quad,
		logical, intent(in)	do_yz_quad,
		logical, intent(in)	do_zx_quad,
		integer, intent(in)	naxes,
		integer, intent(in)	nquad,
		integer, intent(in)	nocts )

–

Base routine to number nodes arround (0,0,0) according to the description Sect. Numbering and Ordering Cartesian neighbors.

The node numbers are written in the stl array argument, whose shape is assumed to be `stl(-n:n, -n:n, -n:n), even in 2D.

The indexing is done in ascending order as decribed in mod_generate_stencil. The starting index is given by the stl_index argument. The array stl is not reset in the process.

Parameters

[in]	n	size of the stl array.
[in,out]	stl
[in,out]	stl_index	first stencil index, updated to the last stencil index plus one.
[in]	spatial_dimension	either 2D or 3D; in 2D, `stl` still have a 3D shape and only `(i,j,0)` nodes are considered.
[in]	do_orig	wether include `(0,0,0)`.
[in]	do_xy_quad	wether include QUAD nodes in the four xy quadrants
[in]	do_yz_quad	wether include QUAD nodes in the four yz quadrants
[in]	do_zx_quad	wether include QUAD nodes in the four zx quadrants
[in]	naxes	extent along the axes.
[in]	nquad	extent along the quadrants.
[in]	nocts	extent along the octants.

◆ shift_stencil_loc()

integer function, dimension(3) mod_generate_stencil::shift_stencil_loc	(	integer, dimension(3), intent(in)	indices,
		integer, dimension(3), intent(in)	direction )

When using staggered arrangements, the logical neighbor indices may not correspond to array indices. In the example below, x-face and y-face nodes are indexed with +/-1. This is the indexing used by generate_stencil. Although, it may not be compatible with arrays storing face node values.

y ↑
 ─┼──^──┼─ j+1
  │     │
  >  o  >  j
  │     │
 ─┼──^──┼─ j-1 → x
     i
 i-1   i+1

For instance, in Notus, the indices are:

y ↑
 ─┼──^──┼─ j+1
  │     │
  >  o  >  j
  │     │
 ─┼──^──┼─ j   → x
     i
  i    i+1

whereas, in Hypre, the indices are:

y ↑
 ─┼──^──┼─ j
  │     │
  >  o  >  j
  │     │
 ─┼──^──┼─ j-1 → x
     i
 i-1    i

Functions/Subroutines